Massachusetts Institute of Technology A. I. Laboratory Artificial Intelligence Memo No. 239 February 29, 1972
HAKMEM
M. Beeler [beeler@bbn.com] R. W. Gosper [rwg@newton.macsyma.com][R. Schroeppel](http://www.cs.arizona.edu/xkernel/www/people/rich.html) [rcs@cs.arizona.edu]
[Retyped and formatted in 'html' ('Web browser format) by Henry Baker, April, 1995. The goal of this 'html' document is to make HAKMEM available to the widest possible audience -- including those without bitmapped graphics browsers. Therefore, equations have been formatted to be readable even on ASCII browsers such as 'lynx'. Click here to get original AI Memo 239 in 400 dots/inch, 1 bit/pixel, Group 4 facsimile TIFF format (a single 5 megabyte gzip compressed tar file, AIM-239.tiff.tar.gz).]
Work reported herein was conducted at the Artificial Intelligence Laboratory, a Massachusetts Institute of Technology research program supported in part by the Advanced Research Projects Agency of the Department of Defense and monitored by the Office of Naval Research under Contract Number N00014-70-A-0362-0002.
Reproduction of this document, in whole or in part, is permitted for any purpose of the United States Government.
Compiled with the hope that a record of the random things people do around here can save some duplication of effort -- except for fun.
Here is some little known data which may be of interest to computer hackers. The items and examples are so sketchy that to decipher them may require more sincerity and curiosity than a non-hacker can muster. Doubtless, little of this is new, but nowadays it's hard to tell. So we must be content to give you an insight, or save you some cycles, and to welcome further contributions of items, new or used.
The classification of items into sections is even more illogical than necessary. This is because later elaborations tend to shift perspective on many items, and this elaboration will (hopefully) continue after publication, since this text is retained in "machinable" form. We forgive in advance anyone deterred by this wretched typography.
People referred to are from the A. I. Lab: ``
Marvin Minsky [minsky@ai.mit.edu]
Bill Gosper [rwg@newton.macsyma.com]
Michael Beeler [beeler@bbn.com]
Joe Cohen
Jerry Freiberg
John Roe
Rich Schroeppel [rcs@cs.arizona.edu]
David Silver
Michael Speciner
Richard Stallman [rms@ai.mit.edu]
Gerald Sussman [gjs@ai.mit.edu]
David WaltzOnce at the A. I. Lab but now elsewhere: ``
Jan Kok William Henneman
Rici Liknaitzky George Mitchell
Peter Samson Stuart Nelson
Roger Banks Rollo Silver
Mike Paterson [Mike.Paterson@dcs.warwick.ac.uk]at Digital Equipment Corporation: ``
Jud Lenard Dave Plumer
Ben Gurley (deceased) Steve Rootelsewhere at M.I.T.: ``
Gene Salamin PDP-1 hackers
Eric Jensen Frances Yao
Edward Fredkinonce at M.I.T., but now elsewhere: ``
Jackson Wright Steve Brown
Malcolm Rayfieldin France: ``
Marco Schutzenberger Henry Cohenat Computer Corporation of America: ``
Bill Mannat BBN: ``
Robert ClementsCAVEATS:
Some of this material is very inside -- many readers will have to excuse cryptic references.
The label "PROBLEM" does not always mean exercise; if no solution is given, it means we couldn't solve it. If you solve a problem in here, let us know.
Unless otherwise stated, all computer programs are in PDP-6/10 assembly language.
GEOMETRY, ALGEBRA, CALCULUS
ITEM 1 (Schroeppel):
(1/3)! and (2/3)! are interexpressible. (1/4)! and (3/4)! are interexpressible.
Thus these two pairs are of dimensionality one.
(1/10)! and (2/10)! are sufficient to express (N/10)! for all N. (1/12)! and (2/12)! are sufficient to express (N/12)! for all N. (1/3)! and (1/4)! are sufficient to express (N/12)! for all N.
Thus the three cases above are of dimensionality two.
PROBLEM: Find some order to this dimensionality business.
The reflection and multiplication formulas:
pi Z
Z! (-Z)! = ---------
sin(pi Z)
(N-1)/2 -NZ-1/2
(2 pi) N (NZ)! = Z! (Z-1/N)! (Z-2/N)! ... (Z-(N-1)/N)!ITEM 2 (Jan Kok):
Problem: Given a regular n-gon with all diagonals drawn, how many regions are there? In particular, how many triple (or N-tuple) concurrences of diagonals are there?
ITEM 3 (Schroeppel):
Regarding convergence of Newton's method for quadratic equations: Draw the perpendicular bisector of the line connecting the two roots. Points on either side converge to the closest root.
On the line:
- they do not converge
- there is a dense set of points which involve division by zero
- there is a dense set of points which loop, but roundoff error propagates so all loops are unstable
- being on the line is also unstable (if the roots are imaginary and you are on the real axis, you may be doing exact computation of the imaginary part (0), hence stay on the line. Example: X^2 + 1 = 0, X0 = random real floating point number.)
ITEM 4 (Schroeppel):
By Mathlab, the discriminant of
4 3 2
X + F X + G X + H X + I is (as the discriminant of
2 2
A X + B X + C is B - 4 A C):
4 3 3 3 3 2 2 2 2
- 27 H + 18 F G H - 4 F H - 4 G H + F G H
2 2 2 2 3 4 2 3
+ I * [144 G H - 6 F H - 80 F G H + 18 F G H + 16 G - 4 F G ]
2 2 2 4
+ I * [- 192 F H - 128 G + 144 F G - 27 F ]
3
- 256 IITEM 5:
In general, the discriminant of an n-th degree polynomial is
/===
! ! 2
! ! (ROOT - ROOT ) = square of determinant whose i,j element is
! ! i j
i < j
i-1
ROOT .
j(The discriminant is the lowest degree symmetric function of the roots which is 0 when any two are equal.)
ITEM 6 (Schroeppel):
If A is the first symmetric function of N variables ``
= X + Y + Z + ...and B is the second symmetric function of N variables ``
= X Y + X Z + ... + Y Z + ...(B = sum of pairs), then ``
2 2 2 2
X + Y + Z + ... = A - 2 B.
3 3 3 3
X + Y + Z + ... = A - 3 A B + 3 C.
4 4 4 4 2 2
X + Y + Z + ... = A - 4 A B + 2 B + 4 A C - 4 D.ITEM 7 (Gosper):
If f(I;X,Y,...) is the Ith symmetric function on N variables, ``
/ 0 if I > N
f(I;X,Y,...) = ! 1 if I = 0
X*f(I-1;Y,Z...) + f(I;Y,Z,...) (N-1 variables)The generating function is simply
N
====
I
> F(I; X, Y, Z) S = (1 + S X) (1 + S Y) (1 + S Z) ...
/
====
I=0ITEM 8 (Schroeppel):
Solutions to
3 2
F(X) = X - 3 B X + C X + D = 0are
------------------------------
/ ------------------
/ F(B) / F(B) 2 F'(B) 3
B - K * 3/ ---- + / [----] + [-----]
V 2 V 2 3
------------------------------
/ ------------------
2 / F(B) / F(B) 2 F'(B) 3
- K * 3/ ---- - / [----] + [-----]
V 2 V 2 3where K is one of the three cuberoots of 1:
1, (-1+sqrt(-3))/2, (-1-sqrt(-3))/2.
ITEM 9 (Schroeppel & Salamin):
If
4 2
X + B X + C X + D = 0,then 2 X = sqrt(Z1) + sqrt(Z2) + sqrt(Z3), where Z1, Z2, Z3 are roots of
3 2 2 2
Z + 2 B Z + (B - 4 D) Z - C = 0.The choices of square roots must satisfy
sqrt(Z1) sqrt(Z2) sqrt(Z3) = -C.
ITEM 10 (Salamin):
An easy solution of
3
-4 X + 3 X - a = 0is X = sin((arcsin a)/3).
In a similar manner, the general quintic can be solved exactly by use of the elliptic modular function and its inverse. See Davis: Intro. to Nonlinear Differential and Integral Equations (Dover), p. 172. Unfortunately, there exists >= 1 typo, since his eqs. (7) and (13) are inconsistent.
ITEM 11 (Salamin):
The following operations generate one-to-one conformal mappings of Euclidean N-space onto itself.
- Translate N-space.
- Expand N-space about one of its points.
- Stereographically project N-space onto an N-sphere, rotate the sphere, then project back onto N-space.
PROBLEMS:
Show that all such conformal maps are generated by these operations for any N. If the one-to-one and onto conditions are removed, then for N = 2, conformal maps can be obtained by analytic functions. Show that for N > 2, no new conformal maps exist.
RECURRENCE RELATIONS
ITEM 12 (Gosper & Salamin): "the Fast Fibonacci Transform"
(motivation for next item)
Define multiplication on ordered pairs
(A,B) (C,D) = (A C + A D + B C, A C + B D).This is just (A X + B) * (C X + D) mod X^2 - X - 1, and so is associative, etc. We note (A,B) (1,0) = (A + B, A), which is the Fibonacci iteration. Thus, (1,0)^N = (FIB(N), FIB(N-1)), which can be computed in log N steps by repeated squaring, for instance. FIB(15) is best computed using N = 16, thus pushing the minimal binary addition chain counterexample to 30 (Liknaitzky). (See Knuth vol. 2, p 398.) By the last formula,
(1,0)^-1 = (FIB(-1),FIB(-2)) = (1, -1),which, as a multiplier, backs up one Fibonacci step (further complicating the addition chain question). Observing that
(1,0)^0 = (FIB(0), FIB(-1)) = (0,1)= the (multiplicative) identity, equate it with scalar 1. Define addition and scalar multiplication as with ordinary vectors.
(A,B)^-1 = (-A, A + B) / (B^2 + A B - A^2),so we can compute rational functions when the denominator isn't zero. Now, by using power series and Newton's method, we can compute fractional Fibonaccis, and even e^(X,Y) and log (X,Y). If we start with (1,0) and square iteratively, the ratio will converge to the larger root of x^2 - x - 1 (= the golden ratio) about as rapidly as with Newton's method.
This method generalizes for other polynomial roots, being an improvement on the method of Bernoulli and Whittaker (Rektorys, Survey of Applicable Math., p. 1172). For the general second order recurrence, F(N+1) = X F(N) + Y F(N-1), we have the multiplication rule: (A,B) (C,D) = (A D + B C + X A C, B D + Y A C).
Inverse: (A,B)^-1 = (-A, X A + B) / (B^2 + X A B - Y A^2).
Two for the price of one: (F(1), Y F(0)) (1,0)^N = (F(N+1), Y F(N))).
ITEM 13 (Salamin & Gosper): LINEAR RECURRENCE RELATIONS
Recurrence relation:
(1) A = C A + ... + C A
k n-1 k-1 0 k-n
with A , ..., A given as initial values.
0 n-1Consider the algebra with basis vectors
0 1 2 n-1
X , X , X , ..., Xand the identification
n n-1 0
(2) X = C X + ... + C X .
n-1 0Thus if U, V, W are vectors and W = U V, then componentwise
====
(3) W = > T U V ,
i / ijk j k
====
j,kwhere the T's depend only on the C's. The following simple procedure yields A(k): express the vector X^k as a linear combination of the basis vectors, then set X^m = A(m) (0<=m<n). Computation of X^k can be done by k-n+1 applications of (2) or by computing the T's in (3) and then applying (3) O(log k) times.
PROOF: If 0 <= k < n, X^k is already a basis vector, so we get A(k). Suppose the procedure works for k < L.
L n L-n
X = X X
n-1 L-n
= (C X + ... + C ) X
n-1 0
L-1 L-n
= C X + ... + C X
n-1 0The procedure evaluates each X^m to A(m), so X^L evaluates to
C A + ... + C A = A . QED
n-1 L-1 0 L-n LThe same procedure will work for negative k using
-1 n-1 n-2
(4) X = (X - C X - ... - C )/C ,
n-1 1 0the unique vector which when multiplied by X yields X^0.
Let (2) be F(X) = 0 and V be the algebra constructed above. Then V is a field iff F(X) is irreducible in the field of the coefficients of V.
PROOF: Note that an element P of V is zero iff P(X) = 0 mod F(X). If G(X) H(X) = F(X), DEG G,H < DEG F, then the product of two non-zero elements is zero and so V can't be a field.
Let P be an arbitrary non-zero element of V.
DEG(GCD(P,F)) <= DEG P < DEG F.
If F(X) is irreducible, then GCD(P,F) = 1, so there exist Q(X), R(X) such that Q(X) P(X) + R(X) F(X) = 1. Then Q(X) P(X) = 1 mod F(X). Since P has an inverse, V is a field.
ITEM 14 (Gosper & Salamin):
Yet another way to rapidly evaluate recurrences is to observe that if
F(N+1) = X * F(N) + Y * F(N-1), then
F(N+2) = (X^2 + 2 Y) * F(N) - Y^2 * F(N-2).This rate doubling formula can be applied iteratively to compute the Nth term in about log N steps, e.g., to get the 69th term given terms 1 and 2, we form 1, 2, 3, 5, 9, 13, 21, 37, 69. This sequence is computed from right to left by iteratively subtracting half the largest possible power of 2. This is sufficient to guarantee that some term further left will differ from the left one by that same (halved) power of 2; e.g., 5, ..., 21, 37 have a common difference of 2^4, so that term 37 can be found from term 5 and term 21 using the fourth application of the rate doubling formula.
The rate tripling formula is F(N+3) = (X^3 + 3 X Y) * F(N) + Y^3 * F(N-3).
For the K-tupling formula:
F(N+K) = P(K) * F(N) + Q(K) * F(N-K) P(K+1) = X * P(K) + Y * P(K-1) (the same recurrence as F) Q(K+1) = -Y * Q(K) P(1) = X Q(1) = Y P(0) = 2 Q(0) = -1 Q(K) = -(-Y)^K P(K) = 2 (-Y)^K/2 * T(K; X/sqrt(-4 Y)), where T(K; X) is the Kth Chebychev polynomial = cos(K arccos X).
If A(I), B(I), and C(I) obey the same second order recurrence, ``
[ A B ] -1 [ C ]
[ I I ] [ I ]
(I) [ ] [ ]
[ A B ] [ C ]
[ J J ] [ J ]is independent of I and J, provided the inverse exists. (This is true even if coefficients are not constant, since any two independent sequences form a basis.)
Plugging in F and P as defined above, we get an expression for the Nth term of the general second order recurrence in terms of P(N) and P(N+1): ``
[ P(N) P(N+1) ] [ P(0) P(1) ] -1 [ F(0) ]
[ P(1) P(2) ] [ F(1) ] = F(N).Setting X = Y = 1, we get FIB(N) = (2 P(N+1) - P(N))/5, which is a complex but otherwise square root free closed form. (sqrt(-4) = 2i)
With constant coefficients, the invariance (I) implies: ``
[ A A ] [ A A ] -1 [ A ]
[ P+I P+J ] [ Q+I+K Q+J+K ] [ R+K ]
[ ] [ ] = A
[ A A ] [ A ] P-Q+R
[ Q+I+L Q+J+L ] [ R+L ]These matrix relations generalize directly for Nth order recurrences.
ITEM 15 (Chebychev):
The Nth Chebychev polynomial T(N) = T(N; x) = cos(N arccos x).
T(0) = 1, T(1) = x, T(N+1) = 2 x T(N) -T(N-1).
T(N; T(M)) clearly = T(N M).
x^N - 2^(1-N) T(N), whose degree is N-2, is the polynomial of degree < N which stays closest to x^N in the interval (-1,1), deviating by at most 2^(1-N) at the N+1 places where x = cos(K * pi/N), K=0, 1, ...N.
Generating function:
====
N 1 - x S
> T(N) S = --------------
/ 2
==== 1 - 2 x S + SFirst order (nonlinear) recurrence:
-------------------
/ 2 2
T(N+1) = x T(N) - /(1 - x ) (1 - T(N) ) .
V(T(N+1),-T(N)) = (T(1),-T(0)) (1,0),
where (A,B) (C,D) = (A D + B C + 2 x A C, B D - A C).
ITEM 16:
``
n n
1 (1+ix) - (1-ix)
tan (n arctan x) = - * -----------------
i n n
(1+ix) + (1-ix)BOOLEAN ALGEBRA
ITEM 17 (Schroeppel):
Problem: synthesize a given logic function or set of functions using the minimum number of two-input AND gates. NOT gates are assumed free. Feedback is not allowed. The given functions are allowed to have X (don't care) entries for some values of the variables. P XOR Q requires three AND gates. MAJORITY(P,Q,R) requires 4 AND gates. "PQRS is a prime number" seems to need seven gates. The hope is that the best Boolean networks for functions might lead to the best algorithms.
ITEM 18 (Speciner):
``
Number of monotonic increasing Boolean
N functions of N variables
- --------------------------------------
0 2 (T, F)
1 3 (T, F, P)
2 6 (T, F, P, Q, P AND Q, P OR Q)
3 20
4 168 = 8 * 3 * 7
5 7581 = 3 * 7 * 19^2
6 7,828,354 = 2 * 359 * 10903 (Ouch!)N from 0 to 4 suggest that a formula should exist, but 5 and 6 are discouraging. A difficult generalization: Given two partial orderings, find the number of maps from one to the other that are compatible with the ordering. A related puzzle: A partition of N is a finite string of non-increasing integers that add up to N. Thus 7 3 3 2 1 1 1 is a partition of 18. Sometimes an infinite string of zeros is extended to the right, filling a half-line. The number of partitions of N, P(N), is a fairly well understood function.
The generating function is
infinity
======
n 1
> P(n) X = ------------------
/ infinity
====== /===
n = 0 ! ! k
! ! (1 - X )
! !
k = 1A planar partition is like a partition, but the entries are in a two-dimensional array (the first quadrant) instead of a string. Entries must be non-increasing in both the x and y directions. A planar partition of 34 would be: ``
1
3 1
3 2 2 1
7 6 4 3 1Zeros fill out the unused portion of the quadrant. The number of planar partitions of n, PL(n), is not a very well understood function.
The generating function is
infinity
======
n 1
> PL(n) X = -------------------
/ infinity
====== /===
n = 0 ! ! k k
! ! (1 - X )
! !
k = 1No simple proof of the generating function is known. Similarly, one can define cubic partitions with entries in the first octant, but no one has been able to discover the generating function. Some counts for cubic partitions and a discussion appear in Knuth, Math. Comp. 1970 or so.
ITEM 19 (Schroeppel):
The 2-NOTs problem: Synthesize a black box which computes NOT-A, NOT-B, and NOT-C from A, B, and C, using an arbitrary number of ANDs and ORs, but only 2 NOTs.
Clue: (Stop! Perhaps you would like to work on this awhile.)
Lemma: Functions synthesizable with one NOT are those where the image of any upward path (through variable space) has at most one decrease (that is, from T to F).
ITEM 20 (Roger Banks):
A Venn diagram for N variables where the shape representing each variable is convex can be made by superimposing successive M-gons (M = 2, 4, 8, ...), every other side of which has been pushed out to the circumscribing circle. If you object to superimposed boundaries, you may shrink the nested M-gons a very slight amount which depends on N.
ITEM 21 (Schroeppel & Waltz):
PROBLEM: Cover the Execuport character raster completely with the minimum number of characters. The three characters I, H and # works. Using capital letters only, the five characters B, I, M, V and X is a minimal solution. Find a general method of solving such problems.
ITEM 22 (Gosper):
PROBLEM: Given several binary numbers, how can one find a mask with a minimal number of 1 bits, which when AND-ed with each of the original numbers preserves their distinctness from each other? What about permuting bit positions for minimum numerical spread, then taking the low several bits?
ITEM 23 (Schroeppel):
(A AND B) + (A OR B) = A + B = (A XOR B) + 2 (A AND B).ITEM 24 (Minsky):
There exists a convex figure n congruent copies of which, for any n, form a Venn diagram of 2^n regions.
RANDOM NUMBERS
ITEM 25 (Schroeppel):
Random number generators, such as Rollo Silver's favorite, which use SHIFTs and XORs, and give as values only some part of their internal state, can be inverted. Also, the outputs may often be used to obtain their total internal state. For example, 2 consecutive values from Rollo's suffice to allow prediction of its entire future. Rollo's is: ``
RANDOM: MOVE A,HI ;register A gets loaded with "high" word
MOVE B,LO ;register B gets loaded with "low" word
MOVEM A,LO ;register A gets stored in "low" word
LSHC A,35. ;shift the 72-bit register AB left 35
XORB A,HI ;bitwise exclusive-or of A and HI replaces bothThis suggests a susceptibility to analysis of mechanical code machines.
See LOOP DETECTOR item in FLOWS AND ITERATED FUNCTIONS section.
ITEM 26 (? via Salamin):
A mathematically exact method of generating a Gaussian distribution from a uniform distribution: let x be uniform on [0,1] and y uniform on [0, 2 pi], x and y independent. Calculate r = sqrt(-log x). Then r cos y and r sin y are two independent Gaussian distributed random numbers.
ITEM 27 (Salamin):
PROBLEM: Generate random unit vectors in N-space uniform on the unit sphere. SOLUTION: Generate N Gaussian random numbers and normalize to unit length.
NUMBER THEORY, PRIMES, PROBABILITY
ITEM 28 (Schroeppel):
After about 40 minutes of run time to verify the absence of any non-trivial factors less than 235, the 125th Mersenne number,
125
2 - 1,was factored on Tuesday, January 5, 1971, in 371 seconds run time as follows:
125
2 - 1 = 31 * 601 * 1801 * 269,089,806,001 * 4,710,883,168,879,506,001.John Brillhart at the University of Arizona had already done this. M137 was factored on Friday, July 9, 1971 in about 50 hours of computer time:
137
2 - 1 = 32,032,215,596,496,435,569 * 5,439,042,183,600,204,290,159.[Current prime records -- H.B.]
ITEM 29 (Schroeppel):
For a random number X, the probability of its largest prime factor being
- greater than sqrt(X)=X^(1/2) is ln 2.
- less than X^(1/3) is about 4.86%.
This suggests that similar probabilities are independent of X; for instance, the probability that the largest prime factor of X is less than X^(1/20) may be a fraction independent of the size of X.
RELEVANT DATA: ([] denote the expected value of adjacent entries.) ``
RANGE COUNT CUMULATIVE SUM OF COUNT
10^12 to 10^6 7198 [6944] 10018
10^6 to 10^4 2466 2820
10^4 to 10^3 354 402 [487]
10^3 to 252 40 48 ;252 = 10^2.4
252 to 100 7 8
100 to 52 1 1 ;52 = 10^1.7
51 to 1 0 0where:
"COUNT" is the number of numbers between 10^12 + 1 and 10^12 + 10018 whose largest prime factor is in "RANGE". The number of primes in 10^12 + 1 to 10^12 + 10018 is 335; the prime number theorem predicts 363 in this range. This is relevant to Knuth's discussion of Legendre's factoring method, vol. 2, p. 351-354.
ITEM 30 (Schroeppel):
Twin primes:
- 166,666,666,667 = (10^12 + 2)/6
- 166,666,666,669
The number 166,666,666,666,667 is prime, but 166,666,666,666,669 is not.
The primes which bracket 10^12 are 10^12 + 39 and 10^12 - 11.
The primes which bracket 10^15 are 10^15 + 37 and 10^15 - 11.
The number 23,333,333,333 is prime.
Various primes, using T = 10^12, are:
40 T + 1, 62.5 T + 1, 200 T - 3, 500 T - 1, 500 T - 7.
ITEM 31 (Schroeppel):
Ramanujan's problem of solutions to
N 2
2 - 7 = Xwas searched to about N = 10^40; only his solutions (N = 3, 4, 5, 7, 15) were found. It has recently been proven that these are the only ones. Another Ramanujan problem: Find all solutions of n! + 1 = x^2.
ITEM 32 (Schroeppel):
Take a random real number and raise it to large powers; we expect the fraction part to be uniformly distributed. Some exceptions:
- phi = (1 + sqrt(5))/2
- all - 1 < X < 1
- sqrt(2) (half are integers, other half are probably uniformly distributed)
1 + sqrt(2) -- Proof:
N N (1 + sqrt(2)) + (1 - sqrt(2)) = integer (by induction); N the (1 - sqrt(2)) goes to zero.- 2 + sqrt(2) -- similar to 1 + sqrt(2)
any algebraic number whose conjugates are all inside the unit circle
Now, 3 + sqrt(2) is suspicious; it looks non-uniform, and seems to have a cluster point at zero. PROBLEM: Is it non-uniform?
ITEM 33 (Schroeppel):
Numbers whose right digit can be repeatedly removed and they are still prime: CONJECTURE: There are a finite number of them in any radix. In decimal there are 51, the longest being 1,979,339,333 and 1,979,339,339.
ITEM 34 (Schroeppel):
PROBLEM: Can every positive integer be expressed in terms of 3 and the operations factorial and integer square root? E.g., 5 = sqrt(sqrt(3!!)).
ITEM 35 (Schroeppel):
Take as many numbers as possible from 1 to N such that no 3 are in arithmetic progression. CONJECTURE: As N - > infinity, the density of such sets approaches zero, probably like
(ln 2)/(ln 3)
N .- XX.XX is a known solution for N = 5
- XX.XX....XX.XX is a known solution for N = 14
Conjecture that XX.XX just keeps getting copied. If the N1 can be proved, it follows that there are infinitely many primes P1, P2, P3 in arithmetic progression, since primes are much more common than N2.
ITEM 36 (Schroeppel):
PROBLEM: How many squares have no zeros in their decimal expression? Ternary?
ITEM 37 (Gosper):
The number of n digit strings base B in which all B digits occur at least once is just the Bth forward difference at 0 of the nth powers of 0, 1, ... . E.g., for n = 4: ``
0 1 16 81 256 625
1 15 65 175 369
14 50 110 194
36 60 84
24 24
0so there are 14 (= 2^4 - 2) such 4-bit strings, 36 such 4-digit ternary strings, 24 (= 4!) such quaternary, and 0 for all higher bases. 27 (= 10e?) random decimal digits are required before it is more likely than not that every digit has occurred; with 50 digits the likelihood is 95%.
ITEM 38 (Fredkin):
By the binomial theorem, the bth forward difference at 0 of the 0, 1, 2, ... powers of n is (n-1)^b. E.g., for n = 4: ``
1 4 16 64 256
3 12 48 192
9 36 144
27 108
81In fact, any straight line with rational slope through such an array will always go through a geometric sequence with common ratio of the form n^a (n-1)^b. In the above, east by southeast knight's moves give the powers of 12: 1, 12, 144, ... .
ITEM 39 (Schutzenberger):
PROBLEM: Using N digits, construct a string of digits which at no time has any segment appearing consecutively twice.
- N = 2 -> finite maximum string
- N = 10 -> known infinite
Determine maximum string length for N = 3.
SUB-PROBLEM: How many sequence exist for any particular length?
ITEM 40 (Gosper):
The variance of a pseudo-Gaussian distributed random variable made by adding T independent, uniformly distributed random integer variables which range from 0 to N-1, inclusive, is T((N^2 - 1)/12).
ITEM 41 (Salamin):
There are exactly 23000 primes less than 2^18.
ITEM 42 (Gosper):
To show that
N
====
L N + 1 N + 1 L
> BINOMIAL(N + L, L) ((1 - X) X + (1 - X) X ) = 1
/
====
L = 0set N to 20 and observe that it is the probability that one or the other player wins at pingpong. (X = probability of first player gaining one point, L = loser's score, deuce rule irrelevant.) If this seems silly, try more conventional methods.
PROBLEM: If somehow you determine A should spot B 6 points for their probabilities of winning to be equal, and B should spot C 9 points, how much should A give C?
ITEM 43 (Schroeppel):
Let (A, B, C, ...) be the multinomial coefficient
(A + B + C....)!
----------------
A! B! C! ...This is equal modulo the prime p to
(A0, B0, C0...) (A1, B1, C1...) (A2, B2, C2...)...where AJ is the Jth from the right digit of A base p.
Thus BINOMIAL(A+B A) mod 2 is 0 iff (AND A B) is not.
The exponent of the largest power of p which divides (A, B, C,...) is equal to the sum of all the carries when the base p expressions for A, B, C, ... are added up.
ITEM 44 (Gosper):
Recurrences for multinomial coefficients:
(A,B,C,...) = (A+B,C,...)(A,B) = (A+B+C,...)(A,B,C) = ...
PROBLEM 45 (Gosper):
- Take a unit step at some heading (angle).
- Double the angle, step again.
- Redouble, step, etc.
For what initial heading angles is your locus bounded?
PARTIAL ANSWER (Schroeppel, Gosper): When the initial angle is a rational multiple of pi, it seems that your locus is bounded (in fact, eventually periodic) iff the denominator contains as a factor the square of an odd prime other than 1093 and 3511, which must occur at least cubed. (This is related to the fact that 1093 and 3511 are the only known primes satisfying
P 2
2 = 2 mod P ).But a denominator of 171 = 9 * 19 never loops, probably because 9 divides phi(19). Similarly for 9009 and 2525. Can someone construct an irrational multiple of pi with a bounded locus? Do such angles form a set of measure zero in the reals, even though the "measure" in the rationals is about .155? About .155 = the fraction of rationals with denominators containing odd primes squared = 1 - product over odd primes of 1 - 1/P(P + 1). This product = .84533064 +- a smidgen, and is not, alas, sqrt(pi/2) ARCERF(1/4) = .84534756. This errs by 16 times the correction factor one expects for 1093 and 3511, and is not even salvaged by the hypothesis that all primes > a million satisfy the congruence. It might, however, be salvaged by quantities like 171.
ITEM 46 (Schroeppel):
The most probably suit distribution in bridge hands is 4-4-3-2, as compared to 4-3-3-3, which is the most evenly distributed. This is because the world likes to have unequal numbers: a thermodynamic effect saying things will not be in the state of lowest energy, but in the state of lowest disordered energy.
ITEM 47 (Beeler):
The Fibonacci series modulo P has been studied. This series has a cycle length L and within this cycle has sub-cycles which are bounded by zero members.
The length of powers of primes seems to be
power-1
L = (length of prime) * prime .The length of products of powers of primes seems to be
L = least common multiple of lengths of powers of primes which are factors.There can be only 1, 2, or 4 sub-cycles in the cycle of a prime.
Primes with 1 sub-cycle seem to have lengths
prime - 1
L = --------- ,
NN covering all integers. Primes with 2 sub-cycles seem to have lengths
M
prime - (-1)
L = ------------- ,
MM covering all integers except of form 10 K + 5.
Primes with 4 sub-cycles seem to always be of form 4 K + 1, and seem to have lengths
prime + 1 prime - 1
L = --------- or --------- ,
R SR covering all integers of form 10 K + 1, 3, 7 or 9; S covering all integers.
At Schroeppel's suggestion, the primes have been separated mod 40, which usually determines their number of sub-cycles: ``
PRIME mod 40 SUB-CYCLES
1, 9 usually 2, occasionally 1 or 4 (about equally)
3, 7, 23, 27 2
11, 19, 31, 39 1
13, 17, 33, 37 4
21, 29 1 or 4 (about equally)
2 (only 2) 1
5 (only 5) 4Attention was directed to primes which are 1 or 9 mod 40 but have 1 or 4 subcycles.
2 2
25 X + 16 Yseems to express those which are 9 mod 40;
2 2
(10 X +- 1) + 400 Yseems to express those which are 1 mod 40.
PROBLEM: Can some of the "seems" above be proved? Also, can a general test be made which will predict exact length for any number?
ITEM 48 (Gosper, Schroeppel):
A point of the 2 dimensional lattice is called visible iff its coordinates are relatively prime. The invisible 2 by 2 square with smallest X has its near corner on (14,20). (I.e., (14,20), (15,20), (14,21), and (15,21) are all invisible.) The corresponding 3 by 3 is at (104,6200). By the chines remainder theorem, there exist invisible sets of every finite shape. Excellent reference: Amer. Math. Monthly, May '71, p487.
ITEM 49:
There is a unique "magic hexagon" of side 3: ``
3 17 18
19 7 1 11
16 2 5 6 9
12 4 8 14
10 13 15First discovered by Clifford W. Adams, who worked on the problem from 1910. In 1957, he found a solution. (See Aug. 1963 Sci. Am., Math. Games.) Other length sides are impossible.
ITEM 50 (Schroeppel):
There is no magic cube of order 4.
Proof: Let K (= 130) be the sum of a row.
Lemma 1: In a magic square of order four, the sum of the corners is K.
Proof: Add together each edge of the square and the two diagonals. This covers the square entirely, and each corner twice again. This adds to 6 K, so twice the corner sum is 2 K.
Lemma 2: In a magic cube of order 4, the sum of any two corners connected by an edge of the cube is K/2.
Proof: Call the corners a and b. Let c, d and e, f be the corners of any two edges of the cube parallel to ab. Then abcd, abef, and cdef are all the corners of magic squares. So a+b+c+d + a+b+e+f + c+d+e+f = 3K; a+b+c+d+e = 3K/2; a+b = K/2.
Proof of magic cube impossibility: Consider a corner x. There are three corners connected by an edge to x.
Each must have value K/2 - x. QED
ITEM 51 (Schroeppel):
By similar reasoning, the center of an order 5 magic cube must be 63 = K/5.
COROLLARY: There is no magic tesseract of order 5.
ITEM 52 (Salamin):
The probability that two random integers are relatively prime is 6/pi^2.
PSEUDO-PROOF: Let X be the probability. Let S be the set of points in the integer lattice whose coordinates are relatively prime, so that S occupies a fraction X of the lattice points. Let S(D) be the set of points whose coordinates have a GCD of D. S(D) is S expanded by a factor of D from the origin. So S(D) occupies a fraction X/D^2 of the lattice, or the probability that two random integers have a GCD of D is X/D^2. If D unequals D', then S(D) intersect S(D') is empty, and union of all S(D) is the entire lattice. Therefore X(1/12+1/22+1/3^2+...) = 1, so X = 6/pi*^2. This argument is not rigorous, but can be made so.
ITEM 53 (Salamin):
The probability that N numbers will lack a Pth power common divisor is 1/zeta(NP).
ITEM 54 (Salamin & Gosper):
The probability that a random rational number has an even denominator is 1/3.
ITEM 55 (Schroeppel): GAUSSIAN INTEGERS
See following illustrations; also PI section.
Figure 1(a). This diagram is to substantiate the claim that every Gaussian integer has a unique bit combination. Running through bit combinations 0, 1, 10, 11, ..., the diagram is a map of values, radix i-1. The origin is circled; the dot is at the 127th combination (1111111 = 2 + 5i), which is merely the last point drawn.
Figure 1(b). As 1(a), but radix i+1. Large circle is origin. Dashes indicate continuity of curve at confusing places. Dotted curve is with an infinity of ones to the left (big dot = ...1111 = i). The solid and dotted curves are symmetrical about the point marked with a small circle.
Figure 2. Similar to 1(a), but showing fraction parts as well. Reprinted by special permission from Knuth, The Art of Computer Programming, Volume 2, Seminumerical Algorithms, 1969, Addison-Wesley, Reading, Mass.
ITEM 56 (Beeler):
The "length" of an N-digit decimal number is defined as the number of times one must iteratively form the product of its digits until one obtains a one-digit product (see Technology Review Puzzle Corner, December 1969 and April 1970). For various N, the following shows the maximum "length", as well as how many distinct numbers (permutation groups of N digits) there are: ``
N MAX L DISTINCT
2 4 54
3 5 219
4 6 714
5 7 2,001
6 7 5,004
7 8 11,439
8 9 24,309
9 9 48,619
10 10 92,377
11 10 167.959
12 10 293,929Also, for N = 10, 11 and 12, a tendency for there to be many fewer numbers of "length" = 7 is noted. Other than this, the frequency of numbers of any given N, through N = 12, decreases with increasing "length", CONJECTURE (Schroeppel): No L > 10.
ITEM 57 (Beeler, Gosper):
There is at least one zero in the decimal expression of each power of 2 between
86 30739014
2 = 77,371,252,455,336,267,181,195,264 and 2 ,where the program was stopped. If digits of such powers were random, the probability that there is another zeroless power would be about 1/10^411816. Assuming there aren't any raises the question:
How many final nonzero digits can a power of two have?
ANSWER (Schroeppel): Arbitrarily many. If we look at the last n digits of consecutive powers of 2, we see:
- None end in zero.
- After the nth, they are all multiples of 2^n.
- They get into a loop of length 4 * 5^(n-1). (Because 2 is a primitive root of powers of 5.)
But there are only 4 * 5(n-1) multiples of 2^n which don't end with zero and are < 10^n, so we will see them all. In particular, we will see the one composed entirely of 1's and 2's, which ends ...11112111211111212122112.
ITEM 58 (Fredkin):
3 3 3 3
3 + 4 + 5 = 6 .ITEM 59 (Schroeppel):
2
91038 90995 89338 00226 07743 74008 17871 09376 =
82880 83126 51085 58711 66119 71699 91017 17324
91038 90995 89338 00226 07743 74008 17871 09376ITEM 60 (Beeler):
If S = the sum of all integers which exactly divide N, including 1 and N, then "perfect numbers" are S = 2 N; the first three numbers which are S = 3 N are:
3
120 = 2 * 3 * 5 = 1111000 base 2
5
672 = 2 * 3 * 7 = 1010100000 base 2
9
523,776 = 2 * 3 * 11 * 31 = 1111111111000000000 base 2ITEM 61 (Root):
Consider iteratively forming the sum of the factors (including 1 but not N) of a number N. This process may loop; "perfect numbers" are those whose loop is one member, N. For example, N = 28 = 1 + 2 + 4 + 7 + 14. An example of a two-member loop is:
- sum of factors of 220 = 284
- sum of factors of 284 = 220
Two-member loops are called "amicable pairs."
A program to search for loops of length > 2, all of whose members are < 6,600,000,000 found the known loops of length 5 (lowest member is 12496) and 28 (lowest member is 14316), but also 13 loops of 4 members (lowest member is given): ``
1,264,460 = 2^2 * 5 * 17 * 3,719
2,115,324 = 2^2 * 3^2 * 67 * 877
2,784,580 = 2^2 * 5 * 29 * 4,801
4,938,136 = 2^3 * 7 * 109 * 809
7,169,104 = 2^4 * 17 * 26,357
18,048,976 = 2^4 * 11 * 102,551
18,656,380 = 2^2 * 5 * 932,819
46,722,700 = 2^2 * 5^2 * 47 * 9,941
81,128,632 = 2^3 * 13 * 19 * 41,057
174,277,820 = 2^2 * 5 * 29 * 487 * 617
209,524,210 = 2 * 5 * 7 * 19 * 263 * 599
330,003,580 = 2^2 * 5 * 16,500,179
498,215,416 = 2^3 * 19 * 47 * 69,739ITEM 62 (Speciner):
The first four perfect numbers are 6, 28, 496, 8128.
Two-member loops (amicable pairs) are: ``
220 <-> 284
1184 <-> 1210
2620 <-> 2924
5020 <-> 5564
6232 <-> 6368
10744 <-> 10856
12285 <-> 14595
17296 <-> 18416
63020 <-> 76084
66928 <-> 66992
67095 <-> 71145
69615 <-> 87633
79750 <-> 88730
100485 <-> 124155
122265 <-> 139815
122368 <-> 123152
141644 <-> 153176
142310 <-> 168730
171856 <-> 176336
176272 <-> 180848
185368 <-> 203432
196724 <-> 202444(Exhaustive to smaller member <= 196724 and larger member < 2^35.)
A prime decade is where N+1, N+3, N+7 and N+9 are all prime. The first occurrence of two prime decades with the theoretical minimum separation is N = 1006300 and N = 1006330. The 335th prime decade is N = 2342770. There are 172400 primes < 2342770.
ITEM 63 (Schroeppel, etc.):
The joys of 239 are as follows:
- pi = 16 arctan (1/5) - 4 arctan(1/239),
- which is related to the fact that 2 * 13^4 - 1 = 239^2,
- which is why 239/169 is an approximant (the 7th) of sqrt(2).
- arctan(1/239) = arctan(1/70) - arctan(1/99) = arctan(1/408)
- arctan(1/577)
- 239 needs 4 squares (the maximum) to express it.
- 239 needs 9 cubes (the maximum, shared only with 23) to express it.
- 239 needs 19 fourth powers (the maximum) to express it.
- (Although 239 doesn't need the maximum number of fifth powers.)
- 1/239 = .00418410041841..., which is related to the fact that
- 1,111,111 = 239 * 4,649.
- The 239th Mersenne number, 2^239 - 1, is known composite, but no factors are known.
- 239 = 11101111 base 2.
- 239 = 22212 base 3.
- 239 = 3233 base 4.
- There are 239 primes < 1500.
- K239 is Mozart's only work for 2 orchestras.
- Guess what memo this is.
- And 239 is prime, of course.
AUTOMATA THEORY
ITEM 64 (Schroeppel):
A 2-counter machine, given N in one of the counters, cannot generate 2^N. Proven Saturday, Sept. 26, 1970. (Independently rediscovered by Frances Yao). But (Minsky, Liknaitzky), given 2^N, it can generate 22N. (A 2-counter machine has a fixed, finite program containing only the instructions "ADD 1", "SUBTRACT 1", "JUMP IF NOT ZERO", which refer to either of two limited counters. Such machines are known universal, but (due to the above) they must have specially encoded inputs.)
ITEM 65 (Schroeppel):
What effort is required to compute pi(X), the number of primes < X? Shanks and Brillhart claim about X^.7.
ITEM 66 (Gosper):
See space-filling curve machine item in TOPOLOGY section.
GAMES
ITEM 67 (Schroeppel):
Regarding "poker coins" game, whose rules are:
- a player throws N coins; he then puts one or more aside and rethrows the rest
- this throwing is repeated until he no longer has any to throw
- highest score (dice) or maximum number of heads (coins) wins
For poker coins, the optimal strategy, with N coins thrown, is:
Z = number of zeros (tails)
- if Z = 0, quit
- if Z = 1, throw the zero
- if 1 < Z < N, save one one, throw the other N-1 coins
- if Z = N, save a zero, throw the other N-1 coins
The optimal strategy for poker dice is hairier.
ITEM 68 (Schroeppel):
PROBLEM: Solve Blackout, a game as follows:
Two players alternate placing X's on a rectangular grid. No two X's may appear adjacent along a side or across the diagonal at a corner. The last X wins.
Some theory: The "indicator" for a position is: make all possible moves from the given position.
Evaluate the indicator of each of these successor positions.
The indicator of the first position is the smallest number which is not the indicator of a successor position. The indicator of the null position is 0. The second player wins iff the indicator is 0. Example of calculating an indicator for the 3 x 3 board: There are 3 distinct moves possible -- corner, side, center. Playing in the center leaves the null position, indicator 0. Playing on the side leaves a 1 x 3 line, indicator 2. Playing in the corner leaves a 3 x 3 L, indicator 3. The smallest number not appearing in our list is 1, so the indicator of a 3 x 3 square is 1. For two boards (not touching) played simultaneously, the indicator is the XOR of the indicators for the separate boards. For any position, the indicator is <= the maximum game length.
PROBLEM: Find some non-exponential way to compute the indicator of a given position. For lines, a period of 34 is entered after the line is about 80 long. For Ls: if one leg is held fixed, the indicator (as a function of the other leg) seems to become periodic with period 34. The time to enter the period becomes greater as the fixed leg increases.
- On an odd x odd board, the 1st player wins.
- On a 4 x N board, the 2nd player wins.
- On a 6 x 6 board, the 1st player wins by playing at the center of one quarter.
This indicator analysis is similar for many other take-away games, such as Nim.
ITEM 69:
Berlekamp of Bell Labs has done the 9 squares (16 dots) Dots game; the 2nd player wins.
ITEM 70:
A neat chess problem, swiped from "Chess for Fun and Chess for Blood", by Edward Lasker:
white: pawns at QN3 and KN7, knight at QN4, bishop at KB7, king at QB2;
black: pawn at QN3, king at QR6. White mates in three moves.
ITEM 71 (Beeler):
There is only one distinct solution to the commercial "Instant Insanity" colored-faces cubes puzzle, which is how it comes packed. (Independently discovered by Dave Plumer.) Mike Paterson has discovered a clever way to solve the puzzle.
ITEM 72 (Beeler):
A window-dice game is as follows:
- The player starts with each of nine windows open, showing the digits 1 - 9.
- Roll two dice.
- Cover up any digits whose sum is the sum on the dice.
- Iterate throwing and closing windows until the equality of sums is impossible.
- Your score is the total of closed windows (highest wins).
An optimum strategy has been tabulated. Usually it is best to take the largest digits possible, but not always; it also depends critically on the remaining numbers.
ITEM 73 (Beeler):
Sim is a game where two players alternately draw lines connecting six dots. The first person can always win, and whether his first move connects with the first player's first move doesn't matter; from there on, however, the strategy branches to a relatively gruesome degree.
PROBLEM: 6 dots is minimum to ensure no stalemate with 2 players; how many dots are required with 3 players?
ITEM 74 (Beeler):
The 4 x 4 game of Nim, also known as Tactix, is a win for the second player, who on his first move can reply center-symmetrically unless the first player's first move was B1 and B2 (analyzed on RLE PDP-1).
ITEM 75 (Gosper, Brown, Rayfield):
A 1963 PDP-1 computer program gave us some interesting data on the traditional game of peg solitaire (33 holes in a plus shape). ``
A B C
D E F
G H I J K L M
N P Q . S T U
V W X Y Z 1 2
3 4 5
6 7 8From the starting position, complement the board. This is the ending position. Now from the starting position, make one move, then complement the board. This is a position one move from a win. By induction, you can win from the complement of any position you can reach. Thus every successful game has a dual game whose positions are the complements of the original ones. This debunks the heuristic of emptying the arms of the plus first and then cleaning up the middle, because there are just as many dual games which empty out the middle first and then the arms! The program found one counterintuitive win which at one point left the center nine empty but had ten in the arms. ``
. B .
D E .
. . . . . . .
. P . . . T U
V W . . . . .
. 4 .
. 7 .By dualizing and permuting a solution from the folklore, we found a similar winning position with 20. (T Q 4 R 1 L J H W Y M J) leaves: ``
A B C
D E F
G H . . . L .
N . . . . . U
V W . . . 1 2
3 . 5
6 7 8then (8 V A C/B 2 6 G M F/K S 8 1 Y V 3 Q A H E).
Another useful observation is that the pegs and their original hole positions fall into four equivalence classes in which they stay throughout the game. Thus the four pegs which can reach the center on the first move are the only ones that ever can. Similarly, the peg jumped over on the last move must be in one of the two classes of eight members which get reduced on the first move. The program's main heuristic was to reduce the larger classes first. ``
a b a
c d c
a b a b a b a
c d c . c d c
a b a b a b a
c d c
a b aWith its heuristics disabled, the program simply scanned lexicographically (left to right in the inner loop, then top to bottom) for a peg which could move. At one point, there is a peg which can move two ways; it chose west. Twelve moves from the end it stopped and went into an exhaustive tree search, in which it found two basically different wins. (Try it yourself.) ``
. . .
. . .
. . . . K . .
. . Q . . . .
. . X Y Z 1 2
3 4 5
6 7 8ITEM 76 (Beeler):
Triangular Hi-Q (or peg solitaire) is 15 pegs in a triangle. Once peg is removed, and thereafter pegs jump others, which are removed. With pegs numbered 1 at the top, 2 and 3 in the next row, etc., ``
REMOVE CAN END WITH ONLY THE PEG
1 1, 7 = 10, 13
2 2, 6, 11, 14
4 3 = 12, 4, 9, 15
5 13Removing only one, no way exists to get to either 1 + 11 + 15 (tips) or 4 + 6 + 13 (centers of sides). Starting with peg 1 removed, 3,016 positions are attainable (not turning board); the sum of ways to get to each of these is 10,306. An example is: remove peg 1, then jump as follows: 6, 13, 10, 1, 2, 11, 14/13, 6, 12/13, 15, 7/4, 13, 4; leaving peg 1.
PROPOSED COMPUTER PROGRAMS, IN ORDER OF INCREASING RUNNING TIME (Schroeppel)
PROBLEM 77:
Count the polyominos up to, say, order 20. From Applied Combinatorial Mathematics, pages 201 and 213: ``
ORDER E. H. NOT ENCLOSING HOLES
1 1 1
2 1 1
3 2 2
4 5 5
5 12 12
6 35 35
7 108 107
8 369 363
9 1285 1248
10 4655 4271
11 17073
12 63600
13 238591
14 901971
15 3426576
16 13079255
17 50107911
18 192622052The order 13 through 18 data is from Computers in Number Theory, 1971, Atkin & Birch, ed., Academic Press, which has not been independently checked. It also gives bounds 3.72 < limit as N goes to infinity of Nth root of number of polyominos of order N (including those enclosing holes) < 4.5. Also an asymptotic formula for the number of polyominos:
N -.98+-.02
4.06 * (N ) * constant.Polyominos may be constructed in 3-space (Soma-like) pieces) or higher dimensions; a curious thought is into how many dimensions does the average, say, 20-omino extend?
PROBLEM 78:
Solve "minichess", chess played on a 5 x 5 board where each side has lost the king's rook, knight, bishop, and 3 pawns, and the opponents are shoved closer together (1 empty row intervening, no double pawn moves).
PROBLEM 79:
Solve the tiger puzzle, a sliding block puzzle mentioned in Scientific American February 1964, pages 122-130.
PROBLEM 80:
Find smallest squared square (a square composed entirely of smaller, unequal squares). Smallest known has 24 small squares (Martin Gardner's Scientific American Book, vol. 2, page 206). See also the following two illustrations. Recently, someone constructed a squared rectangle with sides in the ratio 1:2. It contains 1353 squares.
Figure 3(a). The smallest known (in 1961, and yet today as far as we know) squared square. Reprinted by special permission from Martin Gardner, The Second Scientific American Book of Mathematical Puzzles and Diversions, 1961, Simon and Schuster, New York, New York.
Figure 3(b). A squared rectangle found by Schroeppel using "String Handling Interpretive Translator", a string processing language written by Samson. Sides are 884808 = 2^3 * 3^2 * 12289 and 752225 = 5^2 * 30089; semiperimeter is 1637033 = 419 * 3907. this has 28 squares, which is more than most published squared rectangles.
PROBLEM 81:
Count the magic squares of order 5. There are about 320 million, not counting rotations and reflections.
PROBLEM 82:
List (that is, count) the semigroups of 7 elements; also, the groups of 256 elements (estimated: 11000).
PROBLEM 83 (Gosper):
Compute the integer-valued step function F(R), 0<R<1, the number of circles of radius R which fit into a unit circle. F skips the value 6, and probably 18. How many and how big are the gaps in the range of F? What happens in n dimensions (including n = infinity)?
PROBLEM 84:
Solve pentominos on an 8 x 8 checkerboard game(s).
Rules:
- The checkerboard is for aid in orienting only; black and white are the same.
- The two players may each have a full complement of 12 pentominos, or they may "choose up" their half of one set.
- Players alternate placing pentominos on the board. Pentominos must not overlap.
- The last player to place a pentomino wins.
PROBLEM 85:
With regard to dissection theorems, the following are known: a triangle into a square, 4 pieces (proven minimal); a pentagon into a square, 6 pieces (best known) etc. ("Geometric Dissections" by Harry Lindgreen, Scientific American November 1961). A program can probably check the known dissections for minimality! See following illustration, for example.
Figure 4. A surprising square <--> hexagon dissection, adapted from page 164 of the November, 1961 issue of Scientific American, which see for further diagrams and discussion.
PROBLEM 86:
Find the number of domino coverings for various objects. for example, an asymptotic formula is known for rectangles; also, on a square board, if side mod 4 = 0, coverings appears to be a square; on a square board, if side mode 4 = 2, coverings appears to be twice a square. See Applied Comb. Math., chap. 4.4-4.6, p. 105-121. Article by E. W. Montroll.
PROBLEM 87:
Analyze giveaway chess, which is as follows:
- captures must be made, although you can choose which capture to make
- pawns must be promoted to queens
- king is just another piece
- player to give away all pieces first wins
PROBLEM 88:
Analyze "escalation chess", where white gets 1 move, black 2, white 3, etc. If a player is in check, he must get out of check on his first move. He may not move into check. Taking your opponent's king is verboten, but you can pile up triple checks, etc. A player is checkmated if he can't get his king out of check on his first move.
PROBLEM 89:
In the game "4 pawns", black has 4 pawns, a king, and two moves to white's one. Prove the pawns win. The object in this game is to capture the king. Black is allowed to move through check.
PROBLEM 90:
Solve Scarne's game, "Teeko", which is played on a 5 x 5 board by two players who alternate placing, one at a time, their 4 counters each, after which the counters are moved around (including diagonally). 4 in a row or square wins.
PROBLEM 91:
Solve "five-in-a-row" on an infinite board.
PROBLEM 92:
Solve Tic-Tac-Toe on a 4 x 4 x 4 board. The consensus is a win for the first player, but it's unproven. The first player wins on 4 x 4 x 4 x 4.
PROBLEM 93:
Solve checkers. There are about 10^12 positions. (Computing time currently estimated (Schroeppel) at 1 year).
Programs below this line are considered unfeasible.
PROBLEM 94:
Solve Hex on large boards (11 to 23 on a side); through order 7 have been analyzed by hand. There is a proof that in games where having an extra move can never (repeat: never) hurt you, the worst the first player can be forced to do is draw. Thus, with Hex, in which there is no draw, the first player can always win.
PROBLEM 95:
Solve chess. There are about 10^40 possible positions; in most of them, one side is hopelessly lost.
PROBLEM 96:
Solve Go. About 10^170 positions.
CONTINUED FRACTIONS
ITEM 97 (Schroeppel): CONTINUED FRACTIONS
Simple proofs that certain continued fractions are sqrt(2), sqrt(3), etc. Proof for sqrt(2):
X = [1, 2, 2, 2, ...]
(X-1) (X+1) = [0, 2, 2, 2, ...] * [2, 2, 2, 2, ...] = 1
2
X - 1 = 1
X = sqrt(2)Proof for sqrt(3):
Y = [1, 1, 2, 1, 2, ...]
(Y + 1) (Y - 1) = [2, 1, 2, 1, 2, ...] * [0, 1, 2, 1, 2, ...]
= 2 * [1, 2, 1, 2, 1, ...] * [0, 1, 2, 1, 2, ...] = 2
2
Y - 1 = 2
Y = sqrt(3)Similar proofs exist for sqrt(5) and sqrt(6); but sqrt(7) is hairy.
ITEM 98 (Schroeppel):
The continued fraction expansion of the positive minimum of the factorial function (about 0.46) is
[0, 2, 6, 63, 135, 1, 1, 1, 1, 4, 1, 43, ...].ITEM 99 (Schroeppel):
The value of a continued fraction with partial quotients increasing in arithmetic progression is ``
I (2/D)
A/D
[A+D, A+2D, A+3D, ...] = -------------
I (2/D)
1+(A/D)where the I's are Bessel functions. A special case is ``
I (2)
0
[1, 2, 3, 4, ...] = ----- .
I (2)
1ITEM 100 (Perron):
``
n
/===
! ! 1
! ! (1 + --) =
! ! Ak
k = 1
1 (A1 + 1)A1 (A2 + 1)A2 (A(n-1) + 1)A(n-1)
1 + ----- ---------- ---------- ... ------------------ .
A1 - A1+A2+1 - A2+A3+1 - A(n-1)+An+1ITEM 101A (Gosper):
On the theory that continued fractions are underused, probably because of their unfamiliarity, I offer the following propaganda session on the relative merits of continued fractions versus other numerical representations. For a good cram course in continued fractions, see Knuth, Volume 2, page 316 [1st Edition; s.4.5.3, p. 339 in 2nd Edition]. (In what follows, "regular" means that all numerators are 1, and any radix can be read in place of decimal.)
pi is 3. But not really 3, more like 3 + 1/7. But not really 7, more like 7 + 1/15. But not really 15, ... . So the regular continued fraction for pi is written 3 7 15 1 292 1 1 ... .
The continued fractions for rational numbers always come out even, and rather quickly. Thus, the number of inches per meter is exactly 100/2.54 or 39 2 1 2 2 1 4. The corresponding decimal fraction is 39.3700787... has period 42, making it almost impossible to tell if the number is rational. (But if our data are ALL rational, the ordered pair 5000/127 is even more concise.)
Quadratic surds, which are of course inexpressible as rationals, are generally unrecognizable in decimal. Their continued fractions, on the other hand, are periodic. Nth roots of e^2, ratios of Bessel functions, and ratios of linear functions of these all have regular continued fractions formed by interleaving one or more arithmetic sequences. These special properties will show up regardless of number base. You might recognize 5.436563... as 2e, but even Schroeppel might not notice that 6.1102966796... was ``
2/3 4 e - 2 ---------- 2/3 e - 1
until he wrote it as 6 9 15 21 27 33 ... .
The familiar transcendental functions of rational arguments also have simple continued fractions, but these are generally not regular and cannot be reconstructed from numerical values by a simple algorithm, since nonregular representations aren't unique. The point is, however, that numbers like e, pi, sqrt(2), sin .5, sqrt(7) arctan sqrt(7), etc. can be expressed to unlimited precision by simple programs which produce the terms on demand.
- If we define a rational approximation to be "best" if it comes closer than any other rational with such a small denominator, then continued fractions give the complete set of best rational approximations to the value which they represent. That is, if you truncate a (regular) continue fraction at any point, then the resulting rational number is a best approximation. Furthermore, this remains true if the last term of the approximation is replaced by any smaller positive integer other than
All best approximations can be generated in this manner, in order of increasing denominators (or numerators). For example, the approximants to pi = 3 7 15 1 292 ... are: ``
3: 1/1, 2/1, 3/1 7: (4/1), 7/2, 10/3, 13/4, 16/5, 19/6, 22/7 15: (25/8), 47/15, 69/22, 91/29, 113/36, ... 311/99, 333/106 1: 355/113
... ...
Note that they are all automatically in lowest terms. the size of a denominator is greater than the product of the terms involved and less than the product of the numbers 1 greater than the terms. The approximations are low if the number of terms is odd, high if it's even. (Note that if a 1 ends a continued fraction, it should be added in to the previous term. Thus, to "round off" a continued fraction after a certain term, add in the next term iff it is +-1. In the above, 4/1 and 25/8 correspond to termination with a 1 and are not "best"; 355/113 is "best" because the corresponding term really should be 1.) The error is smaller than 1 over the product of the denominator squared and the first neglected term, so that the total number of digits (numerator and denominator) is usually slightly smaller than with equally accurate decimal fractions. 355/113 is good to 7.5 places instead of 5.5, due to the unusually large term (292) which follows.
Numerical comparison of continue fractions is slightly harder than in decimal, but much easier than with rationals -- just invert the decision as to which is larger whenever the first discrepant terms are even-numbered. Contrast this with the problem of comparing the rationals 113/36 and 355/113.
Regular continued fractions are in 1 to 1 correspondence with the real numbers, unlike decimal (.5 = .49999...) or rationals (2/3 = 6/9, sqrt(6) = ?). Even infinity has a continued fraction, namely, the empty one! (Minus and plus infinity are the same in continued fraction notation.)
Each representation favors certain operations. Decimal favors multiplication by powers of 10. Rationals favor reciprocation, as do continued fractions. To reciprocate a regular continued fraction, add (or if possible, delete) and initial 0 term. To negate, negate all the terms, optionally observing that
-a, -b, -c, -d ... = -a-1, 1, b-1, c, d ... .
- The strongest argument for positional (e.g., decimal or floating) representation for non-integers is that arithmetic is easy. Rational number arithmetic often loses because numerators and denominators grow so large as to require icky multiprecision. Algorithms for arithmetic on continued fractions seem generally unknown. The next items describe how to arithmetically combine continued fractions to produce new ones, one term at a time.
Unfortunately, the effort required to perform these operations manually is several times that for decimal, but the rewards for machine implementation are considerable (which can also be said of floating point). Specifically, these rewards will be seen to be: unlimited significance arithmetic without multiprecision multiplication or division, built in error analysis, immorally easy computation of algebraic functions, no unnecessary computations, no discarding of information (as with roundoff and truncation), reversibility of computations, and the terms of the answer start to come out right away and continue to do so until shut off.
ITEM 101B (Gosper): Continued Fraction Arithmetic
Continued fractions let us perform numerical calculations a little at a time without ever introducing any error, such as roundoff or truncation. As if this weren't enough, the calculations provide automatic error analysis, and obviate most forms of successive approximation. This means we can start with an arithmetic expression like
sqrt(3/pi^2 + e)
-----------------------
tanh(sqrt(5)) - sin(69)and immediately begin to produce the value as a sequence of continued fraction terms (or even decimal digits, if we should be so reactionary), limited only by time and storage. If there are quantities in the expression which are known only approximately, the calculation can provide error bounds on the answer as well as identify the quantity that limited the significance.
All this is possible because each operation (+, /, -, sqrt) in the arithmetic expression requests terms from the continued fractions of its operands only when necessary, and consequently produces terms of its own value as soon as possible. Numbers like pi and e and functions like sin and tanh have continued fraction terms in simple sequences which can be produced by short programs. Imprecise quantities can also be programs which deliver terms until they run out of confidence, whereupon they initiate special action. By then, the last guaranteeable term of the overall expression will have already been produced.
We see then that no calculation is performed unnecessarily, so that, for example, a subexpression which happened to be multiplied by zero would never be evaluated. Also, an operation detecting a deficiency in two or more of its operands provides a natural mechanism for allocating multiprocessor resources, should you have some.
Here are the algorithms for the elementary arithmetic operations on continued fractions.
Let x be a continued fraction
p0 + q0/(p1 + q1/( ... = p0 + q0/x'where x' is again a continued fraction and the p's and q's are integers. We shall call a (p q) pair a "term" of the continued fraction for x. Often, only the p's are mentioned, in which case the q's are implicitly all 1, and x is called a "regular" continued fraction.
Instead of a list of p's and q's, let x be a computer subroutine which produces its next p and q each time it is called. Thus on its first usage x will "output" p0 and q0 and, in effect, change itself into x'. Similarly, let y be another procedurally represented continued fraction r0 + s0/y'. Our problem will be solved if we can write such subroutines for z(x,y) = x+y, x-y, x y, and x/y. When called upon to output a term of z, the subroutine might in turn call for (or "input") terms from x and y until it is satisfied that the unread portions of x and y cannot affect the pending term of z. Then it would output this term and change itself into z', so that it could produce the next term next time. Unfortunately, when we try to do this, our expressions quickly complicate. Let us preempt this complication by computing instead the more general function
z(x,y) = (a x y + b x + c y + d) / (e x y + f x + g y + h)(or
(a b c d) / (e f g h)for short)
where a through h are integer variables whose initial values we are free to choose. Various choices express ``
addition: x + y = (0 1 1 0) / (0 0 0 1),
subtraction: x - y = (0 1 -1 0) / (0 0 0 1),
multiplication: x y = (1 0 0 0) / (0 0 0 1),
division: x / y = (0 1 0 0) / (0 0 1 0).As we shall see, the process of inputting terms of x and y and outputting terms of z will reduce to replacing the eight integers a through h with linear combinations of each other.
When z inputs a term of x, z becomes a new function of x'. To see how this happens, substitute p + q/x' for every occurrence of x in the expression for z(x,y), then multiply numerator and denominator through by x':
z(x',y) = (pa+c pb+d qa qb) / (pe+g pf+h qe qf).If x was rational and has run out of terms, it has in effect become infinite:
z(infinity,y) = (0 0 a b) / (0 0 e f)If instead we input a term of y by substituting r + s/y' for every occurrence of y:
z(x,y') = (ra+b sa rc+d sc) / (re+f se rg+h sg).If y runs out of terms:
z(x,infinity) = (0 a 0 c) / (0 e 0 g)To output the term (t u), so that z = t + u/z' (i.e., z' = u/(z-t)):
z'(x,y) = (ue uf ug uh) / (a-te b-tf c-tg d-th).Thus this basic eight variable form is preserved by all three operations, which can be performed in any order since they represent independent substitutions.
For simplicity, let us assume that z will output in standard form, that is, every u = 1 (regular) and every output term t >= 1 except perhaps the first. This means that z' will always exceed 1 and thus 0 <= u/z' < 1, so that the integer t = z - u/z' must = [z], the greatest integer <= z.
Since z generally varies with x and y, it should not output unless [z] is constant for the range of possible x and y. We can easily compute the range of given the ranges of x and y if we represent each range by the endpoints of an interval (in either order), along with a bit indicating Inside or Outside. Thus if z is in standard form, we can say that z will always be (Inside 1 infinity) (or (Outside -infinity 1)) after the first term. If z were to always output its nearest integer instead of is greatest, then none of the terms after the first would be 1, although they would probably vary in sign. In this case, z would be (Outside -2 2).
Now hold y fixed and examine the behavior of z with x. If x is (Inside a b) then z is (Inside z(a) z(b)) unless the denominator of z changes sign between a and b (i.e., z has its pole in this interval), whereupon z is (Outside z(a) z(b)). Symmetrically, when x is (Outside a b) then z is (Outside z(a) z(b)) unless the signs of the denominators of z(a) and z(b) differ, whereupon z is (Inside z(a) z(b)). This argument still holds with x and y interchanged.
Now suppose that with y fixed at one if its endpoints, x constrains z (Inside 1 2), and at y's other extreme, z(x) is z(y) is (Outside 0 3). Suppose further that at the two extremes of x, z(y) is (Inside 1 3) and (Outside 0 2). Then z(x,y) is (Outside 0 1), the union of the four ranges. (Outside 0 2) is the widest, indicating that z will probably get more information from a term of y than a term of x. (Topology hackers should recognize this Inside-Outside nonsense as ordinary intervals in toroidal space. The clue is that both plus and minus infinity are denoted by the empty continued fraction.)
Due to the basically monotonic behavior of z, we can guarantee that the actual range of z will be the union of these four ranges, and that this range will be Inside or Outside some interval. If it is (Inside z1 z2) and [z1] = [z2], z can output the term t = [z1]. Otherwise, z must input a term from x or y, whichever was associated with the widest of the four ranges of z. (Outside narrowness) is wider than (Outside wideness) is wider than (Inside wideness) is wider than (Inside narrowness).
Evaluating z on these endpoints may be facilitated by keeping estimates for the integer variables in floating point.
Even if z doesn't produce a term, narrowing the range of possible z will still help in computing the range of a function of z, especially if z gets stuck trying to output the last term of a rational number resulting from irrational x and y. (There is no way to guarantee that x or y won't eventually deviate, whereupon z would egest a gigantic term.)
z can produce its value as decimal digits by multiplying by 10 instead of reciprocating, after outputting t = [z]:
z'(x,y) = (10(a-te) 10(b-tf) 10(c-tg) 10(d-th)) / (e f g h).Strange to say, it is not serious if z for some reason outputs the terms 7 5 1 when it should have produced 6 9. As soon as permitted, it will simply recant with 0 -1 -5 and continue with the correction -1 9. The sequence 7 5 1 0 -1 -5 -1 9 is equivalent to 6 9 because b 0 c is the same as b+c. In order to undo these computations, z violates the condition (Outside -1 1) when it is 0 -1 -5 ... . This condition is obeyed by nearly all convergent continued fractions after their first term, and its violation will very probably cause further retractions among the functions dependent upon z.
This computation reversal trick is also handy for mechanizing and denoting imprecise quantities. Instead of 2.997930+-.000003, we have 2 1 481 0 2, meaning between 2 1 481 and 2 1 483. Similarly, 137 26 0 1 replaces 137.0373+-.0006.
Successive approximations methods benefit considerably from not requesting terms until needed. Consider Newton's method for algebraic roots. We expect successive approximations to have about twice as many correct terms each time. Since the production of these terms cannot be aided by reading incorrect terms, the additional correct terms must be produced before the bad ones of the previous approximation are used. But this means that there is no need to read in the bad ones at all. By feeding back the output terms in place of the approximation, we get the correct answer directly! (69% of the credit for this goes to Schroeppel.)
The basic eight variable form exemplified above by z(x,y) is not the only form preserved by continued fraction term transactions. We need only four variables and a single interval check to compute
a x + b
z(x) = ------- ,
c x + dthe homographic function of one argument. On the other hand, z(w,x,y) (linear in all three arguments) requires sixteen variables and a twelve way interval check. Each of these forms can be solved for x in terms of z etc. to get a function of the same form. This is not true of
2
a x + b x + c
z(x) = -------------- ,
2
d x + e x + ffor example, even though this form is also preserved. This form is not guaranteed monotone, thus theoretically invalidating the interval check algorithm, but it hardly every errs. Even if it did, it would quickly correct itself anyway. This form is not only more economical than z(x,x), it is essential for the success of the Newton's method feedback trick, which must know when two variables are really the same one.
By choosing the eight coefficients a through h properly, it should be possible to rewrite arithmetic expressions as compositions of considerably fewer of these forms than one for each +, -, *, and /. The reader is invited to investigate the problem of trying to find minimal representations. Depending on the metric for minimality, the question can be complicated by allowing higher powers of x and y. If the highest powers of x, y, z, ... in an invariant form are i, j, k, .., then the number of integer variables required for the coefficients (mostly because of all the cross terms) is
2 (i+1) (j+1) (k+1) ... .It is awkward in this system to evaluate transcendental functions of irrational arguments. The problem is that you may need any number of continued fraction (or series) terms which, instead of being numbers, are symbolic functions of x, some infinite continued fraction. My suggestion is to represent each symbolic term of the function by a subroutine which is a function of x and the next term, with this next term really a dummy until actually called upon for output, whereupon it replaces itself with a full-fledged term subroutine which in turn refers to x and a new dummy.
Sad to say, the integer variables in these algorithms do not usually shrink on outputs as much as they grow on inputs. Fortunately, the operations for input and output only require (besides addition) multiplication by terms which are almost invariably small. (I have not seen a term exceed 20776 except in specially constructed numbers.) It is fairly safe, then to declare any function which has gotten (Outside -2^35 2^35) to be infinite, thus terminating its continued fraction. Better still, note that the term 20776 is equivalent to the terms 20000 0 700 0 70 0 6, i.e., a very large term can be transmitted piecewise. Although this is just thinly disguised multiprecision multiplication, that first piece of the term will probably satisfy its recipient for quite some time.
In some special cases, the integer variables will become periodic rather than large, especially when all by one of the arguments to a function have terminated. Then, we have the form
a x + b
z(x) = ------- ,
c x + dknown as a homographic function. If ad-bc is +-1, then a, b, c, d will eventually become 1, 0, 0, 1, whereupon z will output the terms of x unmodified. Periodicity will also occur when x is a Hurwitz number, i.e., when the terms of x are the values of one or more polynomials evaluated on consecutive integers and then interleaved. Coth 1/69, sqrt(105), and e are Hurwitz numbers whose polynomials are linear or constant. Hurwitzness is preserved by homographic functions. If one can show that pi is a Hurwitz number, one confirms the long standing conjectures that e**pi,* e+pi, e/pi, etc. are all irrational.
If z, x, and y are all regular, then it generally won't be possible to reduce z by finding a GCD of a through h which is > 1. However, it has been determined empirically that much reduction is often possible in other cases. This reduction is almost always by a divisor of an input or output term numerator (or 10 if output is decimal digits) and can be facilitated by keeping certain of the integer variables around modulo these quantities.
ITEM 101C (Gosper):
Problem: Given an interval, find in it the rational number with the smallest numerator and denominator.
Solution: Express the endpoints as continued fractions. Find the first term where they differ and add 1 to the lesser term, unless it's last. Discard the terms to the right. What's left is the continued fraction for the "smallest" rational in the interval. (If one fraction terminates but matches the other as far as it goes, append an infinity and proceed as above.)
GROUP THEORY
ITEM 102 (Schroeppel):
As opposed to the usual formulation of a group, where you are given
- there exists an I such that A * I = I * A = A, and
- for all A, B and C, (A * B) * C = A * (B * C), and
- for each A there exists an A' such that A * A' = A' * A = I, and
- 4 sometimes you are given that I and A' are unique.
If instead you are given A * I = A and A * A' = I, then the above rules can be derived. But if you are given A * I = A and A' * A = I, then something very much like a group, but not necessarily a group, results. For example, every element is duplicated.
ITEM 103 (Gosper):
The Hamiltonian paths through the N! permutations of N objects using only SWAP (swap any specific pair) and ROTATE (1 position) are as follows: ``
N PATHS + DISTINCT REVERSES
2 2 + 0, namely, S, R
3 2 + 1, namely, SRRSR, RRSRR
4 3 + 3, namely:
SRR RSR SRR RSR RRS RSR RSR RR
RSR SRR RSR RRS RSR RRS RSR RR
SRR RSR RRS RRS RSR RRS RRR SRPROBLEM: A questionable program said there are none for N = 5; is this so?
ITEM 104 (Schroeppel):
Any permutation on 72 bits can be coded with a routine containing only the PDP-6/10 instructions "ROT" and "ROTC".
SET THEORY
ITEM 105 (Komolgoroff, maybe?):
Given a set of real numbers, how many sets can you get using only closure and complement? Answer: 14.
QUATERNIONS
ITEM 107 (Salamin): QUATERNIONS
A quaternion is a 4-tuple which can be regarded as a scalar plus a vector. Quaternions add linearly and multiply (non-commutatively) by
(S1+V1) (S2+V2) = S1 S2 - V1.V2 + S1 V2 + V1 S2 + V1 x V2where S=scalar part, V=vector part, .=dot product, x=cross product.
If Q = S+V = (Q0,Q1,Q2,Q3), then S = Q0, V = (Q1,Q2,Q3). Define conjugation by (S+V)* = S-V. The (absolute value)^2 of a quaternion is
2 2 2 2
Q0 + Q1 + Q2 + Q3 = Q Q* = Q* Q .The non-zero quaternions form a group under multiplication with (1,0,0,0) = 1 as identity and
1 Q*
- = ---- .
Q Q* QThe unit quaternions, which lie on a 3-sphere embedded in 4-space, form a subgroup. The mapping F(Q) = P Q (P a unit quaternion) is a rigid rotation in 4-space. This can be verified by expressing P Q as a 4x4 matrix times the 4-vector Q, and then noting that the matrix is orthogonal. F(Q) restricted to the unit quaternions is a rigid rotation of the 3-sphere, and because this mapping is a group translation, it has no fixed point.
We can define a dot product of quaternions as the dot product of 4-vectors. Then Q1.Q2 = 0 iff Q1 is perpendicular to Q2. Let N be a unit vector. To each unit quaternion Q = S+V, attach the quaternion
N Q = -N.V + N S + N x V .Then it is seen that
(N Q).(N Q) = N.N = 1 and (N Q).Q = 0 .Geometrically this means that N Q is a continuous unit 4-vector field tangent to the 3-sphere. No such tangent vector field exists for the ordinary 2-sphere. Clearly the 1-sphere has such a vector field.
PROBLEM: For which N-spheres does a continuous unit tangent vector field exist?
Let W be a vector (quaternion with zero scalar part) and Q = S+V. Then
Q W Q* = (S^2 + V.V) W + 2 S V x W + 2 V (V.W) .Let N be a unit vector and Q the unit quaternion
Q = +-(cos(theta/2) + N sin(theta/2)) .Then
Q W Q* = (cos theta) W + (sin theta) (N x W) + (1-cos theta) N (N.W) ,which is W rotated thru angle theta about N. If Q thus induces rotation R, then Q1 Q2 induces rotation R1 R2. So the projective 3-sphere (+Q and -Q identified) is isomorphic to the rotation group (3x3 orthogonal matrices). Projectiveness is unavoidable since a 2 pi rotation about any axis changes Q = 1 continuously into Q = -1.
Let U be a neighborhood of the identity in the rotation group (ordinary 3 dimensional rotations) and U1 the corresponding set of unit quaternions in the neighborhood of 1. If a rotation R carries U into U', then a quaternion corresponding to R carries U1 into U1'. But quaternion multiplication is a rigid rotation of the 3-sphere, so U1 and U1' have equal volume. This shows that in the quaternion representation of the rotation group, the Haar measure is the Lebesgue measure on the 3-sphere.
Every rotation is a rotation by some angle theta about some axis. If rotations are chosen "uniformly", what is the probability distribution of theta? By the above, we choose points uniformly on the 3-sphere (or hemisphere since it is really projective). Going into polar coordinates, one finds
2 theta 2
P(theta) = -- (sin -----) , 0 < theta < pi .
pi 2In particular, the expected value of theta is
pi 2
-- + -- .
2 piQuaternions form a convenient 4-parameter representation of rotations, since composition of rotations is done by quaternion multiplication. In contrast, 3-parameter representations like Euler angles or (roll, pitch, yaw) require trigonometry for composition, and orthogonal matrices are 9-parameter. In space guidance systems under development at D-lab, the attitude of the spacecraft is stored in the guidance computer as a quaternion.
POLYOMINOS, ETC.
ITEM 108:
See the PROPOSED COMPUTER PROGRAMS section for counts of polyominos of orders < 19.
ITEM 109 (Schroeppel):
Tessellating the plane with polyominos:
Through all hexominos, the plane can be tessellated with each piece (without even flipping any over). All but the four heptominos below can tessellate the plane, again without being flipped over. Thus, flipping does not buy you anything through order 7. (There are 108 heptominos). ``
H H HHH H H
HHHHH H H HHHH HHHH
HH H H
H HITEM 110 (Schroeppel):
PROBLEM: What rectangles are coverable by various polyominos? For example, ``
XX can cover rectangles which are 3N x M,
X except if N = 1, then M must be even.
YYYY can be shown by coloring to cover only rectangles
having at least one side divisible by four.ITEM 111 (Schroeppel):
PROBLEM: Find a necessary and sufficient condition for an arbitrary shape in the plane to be domino coverable.
ITEM 112 (Beeler):
"Iamonds" are made of equilateral triangles, like diamonds.
"(Poly-)ominos" are made of squares, like dominos.
"Hexafrobs" are made of hexagons.
"Soma-like" pieces are made of cubes.
See also "Polyiamonds", Math. Games, Sci. Am., December 1964. Left and right 3-dimensional forms are counted as distinct. ``
ORDER IAMONDS OMINOS HEXA'S SOMA-LIKE
1 1 1 1 1
2 1 1 1 1
3 1 2 3 2
4 3 5 7 8
5 4 12 22 29
6 12 35
7 24
8 66
9 160
10 448Polyominos of order 1, 2 and 3 cannot form a rectangle. Orders 4 and 6 can be shown to form no rectangles by a checkerboard coloring. Order 5 has several boards and its solutions are documented (Communications of the ACM, October 1965): ``
BOARD DISTINCT SOLUTIONS
3 X 20 2
4 X 15 368
5 X 12 1010
6 X 10 2339 (verified)
two 5 x 6 -- 2
8 x 8 with 2 x 2 hole in center -- 65CONJECTURE (Schroeppel): If the ominos of a given order form rectangles of different shapes, the rectangle which is more nearly square will have more solutions.
Order-4 hexafrob boards and solution counts:
- side 7 triangle -- no solutions
parallelogram, base 7, side 4 -- 9 distinct solutions, e.g., ``
A A A A B C C D E B B C F C D E E B F G G D D E F F G G
Order-6 iamond boards and solution counts (see illustration):
- side 9 triangle with inverted side 3 triangle in center removed -- no solutions
- trapezoid, side 6, bases 3 and 3+6 -- no solutions
- two triangles of side 6 -- no solutions
- trapezoid, side 4, bases 7 and 7+4 -- 76 distinct solutions
- parallelogram, base 6, side 6 -- 156 distinct solutions
- parallelogram, base 4, side 9 -- 37 distinct solutions
- parallelogram, base 3, side 12 --- no solutions
- triangle of side 9 with triangles of side 1, 2 and 2 removed from its corners (a commercial puzzle) -- 5885 distinct solutions
With Soma-like pieces, orders 1, 2 and 3 do not have interesting boxes. Order 4 has 1390 distinct solutions for a 2 x 4 x 4 box. 1124 of these have the four-in-a-row on an edge; the remaining 266 have that piece internal. 320 solutions are due to variations of ten distinct solutions decomposable into two 2 x 2 x 4 boxes. A soma-like 2 x 4 x 4 solution: ``
AAAA BBHH
BCCC BHHC
DDDE FGGE
FDGE FFGEThe commercial Soma has 240 distinct solutions; the booklet which comes with it say this was found years ago on a 7094. Verified by both Beeler and Clements.
TOPOLOGY
ITEM 113:
Although not new (cf Coxeter, Introduction to Geometry, 1st ed. p393), the following coloring number (chromatic number) may be useful to have around:
N = [[(7 + sqrt(48 H + 1))/2]]where N is the number of colors required to color any map on an object which has H holes (note: proof not valid for H = 0).
For example:
- A donut (holes = 1) requires 7 colors to color maps on it.
- A 17-hole frob requires 17 colors.
- An 18-hole frob requires 18 colors.
ITEM 114 (Schroeppel):
A most regular 7-coloring of the torus can be made by tiling the plane with the following repeating pattern of hexagons of 7 colors: ``
A A C C E E
A A A C C C E E E
A A F F C C A A E E
F F F A A A
B B F F D D A A F F
B B B D D D F F F
B B G G D D B B F F
G G G B B B
C C G G E E B B G G
C C C E E E G G G
C C A A E E C C G G
A A A C C C
D D A A F F C C A A
D D D F F F A A A
D D B B F F D D A A
B B B D D D
E E B B G G D D B B
E E E G G G B B B
E E C C G G E E B B
C C C E E E
C C E EDraw an area 7 unit cell parallelogram by connecting, say, the center B's in each of the four ``
B B
B B B 's.
B BFinally, join the opposite sides of the parallelogram to form a torus in the usual (Spacewar) fashion. QUESTION (Gosper): is there a toroidal heptahedron corresponding to this?
ITEM 115 (Gosper):
A spacefilling curve is a continuous map T -> X(T),Y(T), usually from the unit interval onto the unit square, often presented as the limit of a sequence of curves made by iteratively quadrisecting the unit square. Each member of the sequence is then 4 copies of its predecessor, connected in the shape of an inverted V, with the first member being a V which connects 0,0 to 1,0. The limiting map, X(T) and Y(T), can be computed instead by a simple, finite-state machine having 4 inputs (digits of T base 4), 4 outputs (one bit of X and one bit of Y), and 4 states (2 bits) of memory (the number modulo 2 of 0's and 3's seen in T).
Let T, X, and Y be written in binary as: ``
T=.A B A B A B ... X=.X X X X X X ... Y=.Y Y Y Y Y Y ...
1 1 2 2 3 3 1 2 3 4 5 6 1 2 3 4 5 6ALGORITHM S: ``
C <- 0 ;# of 0's mod 4
0
C <- 0 ;# of 3's mod 4
1
S1: X <- A XOR C ;Ith bit of X
I I NOT B
I
Y <- X XOR B ;Ith bit of Y
I I I
C <- C XOR (NOT A AND NOT B ) ;count 00's
0 0 I I
C <- C XOR (A AND B ) ;count 11's
1 1 I I
GO S1
OLD NEW
C C A B X Y C C
0 1 I I I I 0 1
0 0 0 0 0 0 1 0
0 0 0 1 0 1 0 0
0 0 1 0 1 1 0 0
0 0 1 1 1 0 0 1
0 1 0 0 1 1 1 1
0 1 0 1 0 1 0 1 This is the complete
0 1 1 0 0 0 0 1 state transition table.
0 1 1 1 1 0 0 0
1 0 0 0 0 0 0 0
1 0 0 1 1 0 1 0
1 0 1 0 1 1 1 0
1 0 1 1 0 1 1 1
1 1 0 0 1 1 0 1
1 1 0 1 1 0 1 1
1 1 1 0 0 0 1 1
1 1 1 1 0 1 1 0To carry out either the forward or reverse map, label a set of columns as in the table above. Fill in whichever you know of AB or XY, with consecutive rows corresponding to consecutive 1's. Put 0 0 in the top position of the OLD CC column. Exactly one row of the above table will match the row you have written so far. Fill in the rest of the row. Copy the NEW CC entry to the OLD CC column in the next row. Again, only one row of the state table will match, and so forth. For example, the map 5/6 -> (1/2,1/2) (really .11010101... -> (.1000... ,.0111...)): ``
OLD NEW
C C A B X Y C C
0 1 I I I I 0 1
0 0 1 1 1 0 0 1
0 1 0 1 0 1 0 1
0 1 0 1 0 1 0 1
0 1 0 1 0 1 0 1
. . . . . . . .
. . . . . . . .
= 5/6 1/2 1/2We note that since this is a one-to-one map on bit strings, it is not a one-to-one map on real numbers. For instance, there are 2 ways to write 1/2, .1000... and .0111..., and thus 4 ways to write (1/2,1/2), giving 3 distinct inverses, 1/6, 1/2, and 5/6. Since the algorithm is finite state, X and Y are rational iff T is, e.g., 898/4369 -> (1/5,1/3). The parity number, (see SERIES section) and 1-(parity number) are the only reals satisfying X(T)=T, Y(T)=1. This is related to the fact that they have no 0's and 3's base 4, and along with 0, 1/2, and 1=.111..., are the only numbers preserved by the deletion of their even numbered bit positions.
SERIES
ITEM 116 (Schroeppel & Gosper):
inf
====
N! N! 4 2 pi
> ------ = - + --------- .
/ (2 N)! 3 9 SQRT(3)
====
N=0PROBLEM: Evaluate in closed form
inf
====
N! N! N!
> -------- , which =
/ (3 N)!
====
N=0
1
/
[
I (P + Q arccos (R)) dT , where
]
/
0
2 3
2 (8 + 7 T - 7 T )
P = ------------------- and
2 3 2
(4 - T + T )
2 2 3
4 (T - T ) (5 + T - T )
Q = ------------------------------------------ and
2 3 2 2 3
(4 - T + T ) SQRT((4 - T + T ) (1 - T))
2 3
T - T
R = 1 - ------- .
2ITEM 117 (Henry Cohen):
2 3 4
X X X
gamma = - ln X + X - ---- + ---- - ---- ... + ERROR
2 2! 3 3! 4 4!Where ERROR is of the order of (e^-X)/X.
ITEM 118 (Schroeppel):
Differentiate
-Y
Y E = X to get Y + Y X Y' - X Y' = 0.Substitute for Y a power series in X with coefficients to be determined. One observes the curious identity:
N
====
J - 1 N - J N 0
> J (N - J) BINOMIAL(N, J) = N (0 = 1)
/
====
J=1and thus
==== N - 1 N
N X
Y(X) = > ---------
/ N!
====
N=1ITEM 119 (Schroeppel):
PROBLEM: Can someone square some series for pi to give the series
2 ====
pi 1 1 1
-- = -- + -- + ... = > -- ?
6 2 2 / 2
1 2 ==== NITEM 120 (Euler):
The series accelerating transformation
(Abramowitz & Stegun, se. 3.6.27)
==== K K
(-1) (delta A0)
A0 - A1 + A2 - ... = > -----------------
/ K+1
==== 2
K
====
K K-m
(where (DELTA A0) = > BINOMIAL(K, m) (-1) Am = Kth forward difference on A0)
/
====
m=0when applied to
pi 1 1
-- = 1 - - + - - ...
4 3 5gives
==== N-1 2
pi 2 N!
-- = > ----------
4 / (2 N + 1)!
====
N=0Applied to the formula for gamma in Amer. Math. Monthly (vol. 76, #3, Mar69 p273) =
==== T
(- 1) [LOG2(T)]
> ---------------- ([ ] means integer part of)
/ T
====
T=0we get
inf K-1
==== ====
-(K+1) 1
> 2 > ------------------
/ / I
==== ==== BINOMIAL(2 + J, J)
K=1 J=0(Gosper) which converges fast enough for a few hundred digits.
The array of reciprocals of the terms follows, with powers of 2 factored out to the left from all member of each row. ``
4 1
8 1 3
16 1 5 6
32 1 9 15 10
64 1 17 45 35 15
128 1 33 153 165 70 21
256 1 65 561 969 495 126 28The next to left diagonal is 2^(N+1); the perpendicular one 3rd from the right is 1, 9/1= 9, 10/2= 45, 11/3= 165, 12/4= 495.
ITEM 121 (Gosper):
Consider the triangular array: ``
1
1 1
1 4 1
1 11 11 1
1 26 66 26 1
1 57 302 302 57 1This bears an interesting relationship to Pascal's triangle. The 302 in the 4th southeast diagonal and the 3rd southwest one = 426 + 366. Note that rows then sum to factorials rather than powers of 2. If the nth row of the triangle is dotted with any n consecutive elements of (either) n+1st diagonal of Pascal's triangle, we get the nth Bernoulli polynomial: for n = 5, 1(6,i) + 26(6,i+1) + 66(6,i+2) + 26(6,i+3) + 1(6,i+4) = sum of 5th powers of 1 thru i+5, where (j,i) = BINOMIAL (j+i j).
ITEM 122 (Schroeppel, Gosper):
The "parity number" =
inf
====
1 PARITY(N)
- > ---------
2 / N
==== 2
N=0where the parity of N is the sum the bits of N mod 2. The parity number's value is .4124540336401075977..., or, for hexadecimal freaks, .6996966996696996... . It can be written (base 2) in stages by taking the previous stage, complementing, and appending to the previous stage:
.0
.01
.0110
.01101001
.0110100110010110
.01101001100101101001... radix 2i.e.,
stage 0 = 0
N
-2
1 - 2 - stage N
stage N+1 = stage N + ----------------- .
N
2
2If
NUM 0 = 0, DEN 0 = 2
NUM N+1 = ((NUM N)+1) * ((DEN N)-1)
N+1
2 2
DEN N+1 = (DEN N) = 2then
N N
NUM N+1 -2 -2
------- = stage N+1 = (stage N + 2 ) * (1 - 2 ) .
DEN N+1Or, faster, by substituting in the string at any stage:
- the string itself for zeros, and
- the complement of the string for ones.
It is claimed (perhaps proven by Thue?) that the parity number is transcendental.
Its regular continued fraction begins: 0 2 2 2 1 4 3 5 2 1 4 2 1 5 44 1 4 1 2 4 1 1 1 5 14 1 50 15 5 1 1 1 4 2 1 4 1 43 1 4 1 2 1 3 16 1 2 1 2 1 50 1 2 424 1 2 5 2 1 1 1 5 5 2 22 5 1 1 1 1274 3 5 2 1 1 1 4 1 1 15 154 7 2 1 2 2 1 2 1 1 50 1 4 1 2 867374 1 1 1 5 5 1 1 6 1 2 7 2 1650 23 3 1 1 1 2 5 3 84 1 1 1 1284 ... and seems to continue with sporadic large terms in suspicious patterns. A non-regular fraction is
1/(3 -1/(2 -1/(4 -3/(16 -15/(256 -255/(65536 -65535/
N N
2 2
(...2 -(2 -1)/(... .This fraction converges much more rapidly than the regular one, its Nth approximant being
1 + NUM N
--------- ,
1 + DEN Nwhich is, in fact, an approximant of the regular fraction, roughly the 2^N'th.
In addition, 4*(parity number) =
1 3 15 255 65535
2 - - * - * -- * --- * ----- * ...
2 4 16 256 65536This gives still another non-regular fraction per the product conversion item in the CONTINUED FRACTION section.
For another property of the parity number, see the spacefilling curve item in the TOPOLOGY section.
ITEM 123 (Schroeppel, Gosper, Salamin):
ITEM 122 Consider the image of the circle |z| = 1 under the function
n
=== 2
z
f(z) = > --- .
/ n
=== 2This is physically analogous to a series of clock hands placed end to end. The first hand rotates around the center (0,0) at some rate. the next hand is half as long and rotates around the end of the first hand at twice this rate. The third hand rotates around the end of the second at four times this rate; etc. It would seem that the end of the "last" hand (really there are infinitely many) would sweep through space very fast, tracing out an (infinitely) long curve in the time the first hand rotates once. The hands shrink, however, because of the 2^n in the denominator. Thus it is unclear whether the curve's arc length is really infinite.
Also, it is a visually interesting curve, as are
=== n! === FIB(n)
z z
f(z) = > --- and f(z) = > ------- .
/ n! / FIB(n)
=== ===Gosper has programmed the one mentioned first, which makes an intriguing display pattern. see following illustrations. If you write a program to display this, be sure to allow easy changing of:
- z and z* on alternate terms (alternate hands rotate in opposite directions),
- negation of alternate terms (alternate hands initially point in opposite directions), and
- how many terms are used in the computation, since these cause fascinating variations in the resulting curve.
Figure 6(a). Image of circles |z| = 1/2, 3/4, 7/8, 1 under the function
inf
=== n!
z
f(z) = > --- .
/ n!
===
n=1Figure 6(b). Image of circles |z| = 1/8, 2/8, ..., 8/8 under the function
inf n
=== 2
z
f(z) = > --- .
/ n
=== 2
n=0Both [original] plots by Salamin on the RLE PDP-1.
ITEM 124 (Schroeppel):
Consider
==== ==== ====
1 1 1 1 1
> -- = > (-- - ------) + > (----- - -----) =
/ 2 / 2 2 1 / 1 1
==== N ==== N N - - ==== N - - N + -
4 2 2ITEM 122 ==== 1 2 - > ------------- . / 2 2 ==== N (4 N - 1)
Take the last sum and re-apply this transformation. This may be a winner for computing the original sum. For example, the next iteration gives
====
31 1
-- - 9 > --------------------------------
18 / 2 2 4 2
==== N (4 N - 1) (25 N + 5 N + 9)
where the denominator also =
2 2 2
N (2 N - 1) (2 N + 1) (5 N - 5 N + 3) (5 N + 5 N + 3)ITEM 125 (Polya):
CONJECTURE: If a function has a power series with integer coefficients and radius of convergence 1, then either the function is rational or the unit circle is a natural boundary.
Reference: Polya, Mathematics and Plausible Reasoning, volume 2, page 46.
FLOWS AND ITERATED FUNCTIONS
ITEM 126 (Schroeppel):
An analytic flow for Newton's method square root:
2
X + K
Define F(X) by ------ ; then
2 X
N N
2 2
(X + sqrt(K)) + (X - sqrt(K))
F(F(F(...(X)))) = sqrt(k) ---------------------------------
N N
2 2
(X + sqrt(K)) - (X - sqrt(K))
which = sqrt(K) (coth 2 (arccoth X/sqrt(K))).ITEM 127 (Schroeppel):
P and Q are polynomials in X; when does P(Q(X)) = Q(P(X)) ? (That is, P composed with Q = Q composed with P.)
Known solutions are:
- Various linear things.
- X to different powers, sometimes multiplied by roots of 1.
- P and Q are each another polynomial R composed with itself different numbers of times.
Solutions arising out of the flow of X^2 - 2, as follows:
suppose X = Y + 1/Y, then Y^N + Y^-N can be written as a polynomial in X.
For example, P = the expression for squares = X^2 - 2 (N = 2) and Q = the expression for cubes = X^3 - 3 X (N = 3)
- Replace X by Y-A, then add A to the original constants in both P and Q. For example, P = X^2 and Q = X^3, then P = 1 + (Y-1)^2 = Y^2 - 2 Y + 2 and Q = 1 + (Y-1)^3, then P(Q) = 1 + (Y-1)^6 = Q(P). Similarly, replacing X with A Y + B works.
There are no more through degrees 3 and 4 (checked with Mathlab); but are there any more at all?
ITEM 128 (Schroeppel):
Figure 7. A map of the process n-> binary string -> interpret as radix -2, iterated. To convert a number to base -2:
(n + ...101010) XOR (...101010) (reversible).
ITEM 129 (Schroeppel):
PROBLEM: Given F(X) as a power series in X with constant term = 0, write the flow power series.
FLOW sub ZERO = X
FLOW sub ONE = F(X)
FLOW sub TWO = F(F(X))
etc.NOTE (Gosper): If we remove the restriction that F has a power series, the functions that satisfy an equation of the form F(F(X)) = sin X can be put into one-to-one correspondence with the set of all functions.
ITEM 130 (Salamin):
If F(X) = X^N, the P-th flow is XNP, which has a branch point if N^P is non-integer. Under the hypotheses of the previous problem, it is possible to find the power series coefficients for P rational, but there is no guarantee the series will converge.
PROBLEM: Is the flow interpolation unique? If it is not, what extra conditions are necessary to make it unique for natural cases like X^N ?
ITEM 131 (Schroeppel):
Taking any two numbers A and B, finding their arithmetic mean and their geometric mean, and using these means as a new A and B, this process, when repeated, will approach a limit which can be expressed in terms of elliptic integrals. (See PI section.)
ITEM 132 (Gosper): LOOP DETECTOR
If a function F maps a finite set into itself, then its flow must always be cyclic. If F is one step of a pseudorandom number generator, or the CDR operation on a self referent list, or any function where it is easy to supply former values as arguments, then there are easy ways to detect looping of the flow (Knuth, The Art of Computer Programming, volume 2, Seminumerical Algorithms, sec. 3.1, prob. 7, page 7). If, however, the process or iterated application of the function is inexorable, (i.e., there is no easy way to switch arguments to the function), then the following algorithm will detect repetition before the third occurrence of any value.
Set aside a table TAB(J), 0 <= J <= log 2 (Largest possible period). Let C = the number of time F has been applied, initially 0. Compare each new value of F for equality with those table entries which contain old values of F. These will be the first S entries, where S is the number of times C can be right shifted before becoming 0. No match means F hasn't been looping very long, so increment C and store this latest value of F into TAB(J), where J is the number of trailing zero bits in the binary of C. (The first 16 values of J are: 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, 4, ...; Eric Jensen calls this the RULER function.) A match with entry E means the loop length is 1 more than the low E+2 bits of C - 2^(E+1).
ITEM 133 (Schroeppel, Gosper, Henneman & Banks) (from Dana Scott?):
The "3N+1 problem" is iteratively replacing N by N/2 if N is even or by 3 N + 1 if N is odd. Known loops for N to fall into are:
- 1 the zero loop, 0 -> 0
- 2 a positive loop, 4 -> 2 -> 1 -> 4
- 3 three negative loops (equivalent to the 3N-1 problem with positive N)
- -2 -> -1 -> -2
- -5 -> -7 -> -10 -> -5
- -17 -> -25 -> -37 -> -55 -> -82 -> -41 -> -61 -> -91 -> -136 -> -68 -> -34 -> -17
In the range -10^8 < N < 6 * 10^7, all N fall into the above loops. Are there any other loops? Does N ever diverge to infinity?
ITEM 134 (Schroeppel, Gosper):
Let N be iteratively replaced by (FLATSIZE (LONGHAND N)), the number of letters in N written longhand (e.g., 69 -> SIXTY NINE -> 9 (10 counting blanks)). The process invariably loops at 4 = FOUR.
ITEM 135 (Gosper): The "C" Curve
A brilliant archeologist is photographing a strange drawing on the wall of a cave. He holds the camera upright for some shots, moves it, and turns it 90 degrees for the rest. When he sees is prints he is amazed to find one of them apparently taken with the camera turned 45 degrees. After a moment's reflection, he correctly concludes that it is merely a double exposure.
What was the drawing?
Answer: It is a cousin to both the dragon and snowflake curves (and arose as a bug in a spacefilling curve). It can be constructed as follows. Start with a line segment. Replace it with the two legs of the isosceles right triangle of which it is the hypotenuse. Repeat this for the two new segments, always bulging outward in the same direction. We now have four segments forming half a square, with the middle two segments collinear. Replacing these four segments with eight and then sixteen, we find the middle two segments superimposed. As the process continues, the curve crosses itself more and more often, eventually taking on the shape of a wildly curly letter C which forms the envelope of a myriad of epicyclic octagons.
A faster way to approach the same limiting curve is to substitute the curve itself for each of its 22n segments, starting with a 90 degree "<".
Yet another way to construct it is to iteratively connect opposite ends of two copies at a 90 degree angle. (The archeologist did this with his double exposure.) If we reduce the scale by sqrt(2) each time, the distance between the endpoints stays the same. If the initial line segment is red and there is some other blue shape elsewhere in the picture, the iteration will simultaneously proliferate and shrink the blue shapes, until they are all piled up along the red "C". Thus, no matter what you start with, you eventually get something that looks like the "C" curve.
There are other pictures besides the C curve which are preserved by this process, but they are of infinite size. You can get them by starting with anything and running the iteration backwards as well as forwards, superimposing all the results. A backward step consists of rotating the two copies in directions opposite those in the forward step and stretching by sqrt(2) instead of shrinking. David silver has sketched an arrangement of mirrors which might do this to a real scene.
Figure 8. Two orders of the "C" curve.
PI
ITEM 136: GAUSSIAN INTEGERS (For use by next item.)
Reference: Hardy and Wright, Theory of Numbers. The Gaussian integers are x+iy where x and y are integers. Unique factorization holds, except for powers of i, and the Gaussian primes are
- a+bi if a2+b2 is prime and
- integer primes that = 3 mod 4.
If N(x+iy) = x2+y2, then N(u v) = N(u) N(v). If p is prime and not= 3 mod 4, then p = a2+b2 has exactly one solution. If n = 3 mod 4, then n = a2+b2 has no solution.
To factor x+iy into Gaussian primes, first factor N(x+iy).
- If 2 divides N(x+iy), then 1+i and 1-i divide x+iy. Either factor may be used since i (i-1) = i+1.
- if p = 3 mod 4 divides N(x+iy), then p divides x+iy.
- If p = 1 mod 4 divides N(x+iy) and p = a2+b2, then a+ib or b+ia = i (a-ib) divides x+iy. If both do, then p divides x+iy.
ITEM 137 (Salamin): GENERATION OF ARCTANGENT FORMULAS FOR PI
n1 atan(y1/x1) + n2 atan(y2/x2) + ... = n1 arg(x1+iy1) + n2 arg(x2+iy2) + ...
If each x+iy is factored and the n's chosen so all prime factors except 1+i cancel out, the right hand side is a multiple K of pi/4. Some care is needed because of the multiple valuedness of arg. Then, if K = 0, we get an arctangent identity, otherwise we get a pi formula. In the special case of atan(1/x), factorization of x+i is needed. Then case (B) above can't occur, and in case (C), a+ib and a-ib can't both divide x+i.
Example:
2
8 + 1 = 13 x 5
2 2
18 + 1 = 13 x 5
2 3
57 + 1 = 13 x 5 x 2From this we get the factorization
8+i = (3+2i) (2-i)
2
18+i = (3-2i) (2-i) i
3
57+i = (3-2i) (2+i) (1-i)Since we only care about the phase, multiplication by a positive real number may be ignored below.
a b c a-b-c -a-2b+3c c b
(8+i) (18+i) (57+i) = (3+2i) (2+i) (1-i) iWe require a-b-c = 0 and -a-2b+3c = 0, which has the minimal non-trivial solution a = 5, b = 2, c = 3. Then we have
5 2 3 3 2
(8+i) (18+i) (57+i) = (1-i) iTaking the phase of both sides, we get
5 atan(1/8) + 2 atan(1/18) + 3 atan(1/57) = pi/4.pi formulas:
pi/4 = atan(1/2) + atan(1/3)
pi/4 = 2 atan(1/3) + atan(1/7)
pi/4 = 4 atan(1/5) - atan(1/239)
pi/4 = 2 atan(1/4) + atan(1/7) + 2 atan(1/13)
pi/4 = 3 atan(1/4) + atan(1/13) - atan(1/38)
pi/4 = 4 atan(1/5) - atan(1/70) + atan(1/99)
pi/4 = 5 atan(1/8) + 2 atan(1/18) + 3 atan(1/57)
pi/2 = 7 atan(1/4) - 5 atan(1/32) + 3 atan(1/132) - 4 atan(1/378)This last angle has been measured against the International Standard Platinum-Iridium Right angle and certified adequate for any purpose of the U.S. Government, when used in conjunction with a conscientiously applied program of oral hygiene and regular professional care.
pi/4 = 7 atan(1/9) + atan(1/32) - 2 atan(1/132) - 2 atan(1/378)
pi/4 = 7 atan(1/13) + 8 atan(1/32) - 2 atan(1/132) + 5 atan(1/378)There are many easily found arctangent identities. Some are:
atan(1/31) = atan(1/57) + atan(1/68)
= atan(1/44) + atan(1/105)
atan(1/50) = atan(1/91) + atan(1/111)
atan(1/239) = atan(1/70) - atan(1/99)
= atan(1/408) + atan(1/577)
atan(1/2441) = atan(1/1164) - atan(1/2225)
= atan(1/4774) + atan(1/4995)
atan(1/32) = atan(1/38) + atan(1/132) - atan(1/378)
= 2 atan(1/73) + atan(1/239) - atan(1/2943)Infinite sets of arctangent identities:
1 1 1
atan(-) - atan(---) = atan(------)
n n+1 2
n +n+1Let x(0) = 1, y(0) = 0, x(n) = x(n-1) + 2 y(n-1), y(n) = x(n-1) + y(n-1).
x(n)/y(n) are the continued fraction approximants to sqrt(2).
1 1 1
atan(-----) + atan(-----) = atan(-------)
y(2n) x(2n) x(2n-1)
1 1 1
atan(-----) - atan(-----) = atan(-------)
y(2n) x(2n) x(2n+1)ITEM 138 (Gosper):
pi = 28 arctan (3/79) + 20 arctan (29/278)
pi = 48 arctan (3/79) + 20 arctan (1459/22049)
Which isn't too interesting except that it means that
48 20
(79+3i) (22049+1457i)is a negative real number.
ITEM 139 (Ramanujan):
4
-- =
pi
inf
==== N
(-1) (1123 + 21460 N) (1 3 5 ... (2N-1)) (1 3 5 ... (4N-1))
> ------------------------------------------------------------
/ 2N+1 N 3
==== 882 32 N!
N=0This series gives about 6 decimal places accuracy per term.
1
---------- =
sqrt(8) pi
inf
====
(1103 + 26390 N) (1 3 5 ... (2N-1)) (1 3 5 ... (4N-1))
> ------------------------------------------------------
/ 4N+2 N 3
==== 99 32 N!
N=0This series gives about 8 decimal places accuracy per term. For other pi series, see Ramanujan's paper "Modular Equations and Approximations to Pi" in Quarterly Journal of Pure and Applied Mathematics, vol. 45, page 350 (1914). For more goodies, see "Collected Papers of Srinivasa Ramanujan", Cambridge U. Press (1927).
ITEM 140:
Counting the initial 3 as the zeroth, the 431st denominator in the regular continued fraction for pi is 20776. (Choong, Daykin & Rathbone, Math. of Computation 25 (1971) p. 387).
(Gosper) In the first 26491 terms of pi, the only other 5 digit terms are the 15543rd = 19055 and the 23398th = 19308. (Computed from 35570 terms of the (nonregular) fraction for 4 arctan 1.)
ITEM 141:
The fraction part of 10^760 pi begins: .49999998...
ITEM 142 (Salamin):
Some super-fast convergents to pi if one already has a super-fast computation of trig functions.
X approx pi:
- X <- X + sin X, epsilon <- epsilon^3/6
- X <- X - tan X, epsilon <- -epsilon^3/3
X approx pi/2:
- X <- X + cos X, epsilon <- epsilon^3/6
- X <- X + cot X, epsilon <- -epsilon^3/3
ITEM 143 (Salamin):
Computation of elliptic integrals, log, and pi.
REFERENCES
- Whittaker & Watson, Modern Analysis, chap. 22.
- Abramowitz & Stegun, Handbook of Mathematical Functions, sect. 17.3, 17.6
1. ELLIPTIC INTEGRALS
Define elliptic integrals:
1
/
[ 1
K(m) = I ------------------------- dt
] 2 2
/ sqrt((1 - t ) (1 - m t ))
0
K'(m) = K(1 - m).If A(0) and B(0) are given, and
- A(n+1) = arithmetic mean of A(n) and B(n)
- B(n+1) = geometric mean of A(n) and B(n)
then define
AGM(A(0),B(0)) = lim A(n) = lim B(n)
This is called the arithmetic-geometric mean.
Quadratic convergence rate:
2
(A(n)-B(n))
A(n+1) - B(n+1) = -----------
8A(n+1)It is known that
2 pi
K'(x ) AGM(1, x) = -- [see A&S]
2This gives a super fast method of computing elliptic integrals. It is easy to compute AGM(1, x) for x in the complex plane cut from zero to infinity along the negative real axis. So K'(m) can be computed for -2pi < arg(m) < 2pi, which covers the complex m-plane twice. Handling the phase when taking square roots will permit exploration of more of the Riemann surface.
2. LOGARITHMS
For small m,
K(m) = (pi/2) (1 + m/4 + O(m^2))
e^-pi(K'(m)/K(m)) = (m/16) (1 + m/2 + O(m^2))
Solve for K'(m) and let m = 16/x^2.
K'(16/x^2) = log x + (4/x^2) (log x - 1) + O(log x/x^4).
For x sufficiently large,
log x = K'(16/x^2) = pi/(2 AGM(1, 4/x)).
Requiring a given number of bits accuracy in log x is equivalent to requiring
|K'(16/x^2) - log x)/log x| < epsilon
this becomes
|(4/x^2) (1 - 1/log x)| < |4/x^2| < epsilon
|x| > 2/sqrt(epsilon).
x can be complex. If |x| is not too close to 1, x can be brought into range by reciprocating or repeated squaring.
3. PI
let x = e^n, then
pi = 2 n AGM(1, 4 e^-n).
Suppose epsilon = 10 to the minus a billion.
Than the above equation for pi is valid when n > 1.15 billion.
e^-n is calculated by starting with 1/e and squaring k times.
Thus n = 2^k. 2^30 = 1.07 billion and 2^31 = 2.15 billion, so k = 30 gives 0.93 billion places accuracy and k = 31 gives 1.86 billion places.
ITEM 144 (Schroeppel):
In the above, instead of x = e^n, use x = 2^n and x = *e**2^n. Then simultaneous equations can be solve to give both pi and log 2. This avoids having to square e, but requires two AGM's, and therefore takes longer.
PROGRAMMING HACKS
WARNING: Numbers in this section are octal (and occasionally binary) unless followed by a decimal point. 105=69.. (And 105.=69 hexadecimal.) [PDP-10 Info]
ITEM 145 (Gosper):
Proving that short programs are neither trivial nor exhausted yet, there is the following: ``
0/ TLCA 1,1(1)
1/ see below
2/ ROT 1,9
3/ JRST 0This is a display hack (that is, it makes pretty patterns) with the low 9 bits = Y and the 9 next higher = X; also, it makes interesting, related noises with a stereo amplifier hooked to the X and Y signals. Recommended variations include: ``
CHANGE: GOOD INITIAL CONTENTS OF 1:
none 377767,,377767; 757777,,757757; etc.
TLC 1,2(1) 373777,,0; 300000,,0
TLC 1,3(1) -2,,-2; -5,,-1; -6,,-1
ROT 1,1 7,,7; A0000B,,A0000B
ROTC 1,11 ;Can't use TLCA over data.
AOJA 1,0ITEM 146: MUNCHING SQUARES
Another simple display program. It is thought that this was discovered by Jackson Wright on the RLE PDP-1 circa 1962. ``
DATAI 2
ADDB 1,2
ROTC 2,-22
XOR 1,2
JRST .-42=X, 3=Y. Try things like 1001002 in data switches. This also does interesting things with operations other than XOR, and rotations other than -22. (Try IOR; AND; TSC; FADR; FDV(!); ROT -14, -9, -20, ...)
ITEM 147 (Schroeppel):
Munching squares is just views of the graph Y = X XOR T for consecutive values of T = time.
ITEM 148 (Cohen, Beeler):
A modification to munching squares which reveals them in frozen states through opening and closing curtains: insert FADR 2,1 before the XOR. Try data switches = ``
4000,,4 1000,,2002 2000,,4 0,,1002(Notation: <left half>,,<right half>)
Also try the FADR after the XOR, switches = 1001,,1.
ITEM 149 (Minsky): CIRCLE ALGORITHM
Here is an elegant way to draw almost circles on a point-plotting display:
NEW X = OLD X - epsilon * OLD Y NEW Y = OLD Y + epsilon * NEW(!) X
This makes a very round ellipse centered at the origin with its size determined by the initial point. epsilon determines the angular velocity of the circulating point, and slightly affects the eccentricity. If epsilon is a power of 2, then we don't even need multiplication, let alone square roots, sines, and cosines! The "circle" will be perfectly stable because the points soon become periodic.
The circle algorithm was invented by mistake when I tried to save one register in a display hack! Ben Gurley had an amazing display hack using only about six or seven instructions, and it was a great wonder. But it was basically line-oriented. It occurred to me that it would be exciting to have curves, and I was trying to get a curve display hack with minimal instructions.
ITEM 150 (Schroeppel):
PROBLEM: Although the reason for the circle algorithm's stability is unclear, what is the number of distinct sets of radii? (Note: algorithm is invertible, so all points have predecessors.)
ITEM 151 (Gosper):
Separating X from Y in the above recurrence,
X(N+1) = (2 - epsilon^2) * X(N) - X(N-1) Y(N+1) = (2 - epsilon) * Y(N) - Y(N-1).
These are just the Chebychev recurrence with cos theta (the angular increment) = 1-epsilon^2/2. Thus X(N) and Y(N) are expressible in the form R cos(N theta + phi). The phi's and R for X(N) and Y(N) can be found from N=0,1. The phi's will differ by less than pi/2 so that the curve is not really a circle. The algorithm is useful nevertheless, because it needs no sine or square root function, even to get started.
X(N) and Y(N) are also expressible in closed form in the algebra of ordered pairs described under linear recurrences, but they lack the remarkable numerical stability of the "simultaneous" form of the recurrence.
ITEM 152 (Salamin):
With exact arithmetic, the circle algorithm is stable iff |epsilon| < 2. In this case, all points lie on the ellipse
X^2 - epsilon X Y + Y^2 = constant,
where the constant is determined by the initial point. This ellipse has its major axis at 45 degrees (if epsilon > 0) or 135 degrees (if epsilon < 0) and has eccentricity
sqrt(epsilon/(1 + epsilon/2)).
ITEM 153 (Minsky):
To portray a 3-dimensional solid on a 2-dimensional display, we can use a single circle algorithm to compute orbits for the corners to follow. The (positive or negative) radius of each orbit is determined by the distance (forward or backward) from some origin to that corner. The solid will appear to wobble rigidly about the origin, instead of simply rotating.
ITEM 154 (Gosper):
The myth that any given programming language is machine independent is easily exploded by computing the sum of powers of 2.
- If the result loops with period = 1 with sign +, you are on a sign-magnitude machine.
- If the result loops with period = 1 at -1, you are on a twos-complement machine.
- If the result loops with period > 1, including the beginning, you are on a ones-complement machine.
- If the result loops with period > 1, not including the beginning, your machine isn't binary -- the pattern should tell you the base.
- If you run out of memory, you are on a string or Bignum system.
- If arithmetic overflow is a fatal error, some fascist pig with a read-only mind is trying to enforce machine independence. But the very ability to trap overflow is machine dependent.
By this strategy, consider the universe, or, more precisely, algebra:
let X = the sum of many powers of two = ...111111 now add X to itself; X + X = ...111110 thus, 2X = X - 1 so X = -1 therefore algebra is run on a machine (the universe) which is twos-complement.
ITEM 155 (Liknaitzky):
To subtract the right half of an accumulator from the left (as in restarting an AOBJN counter): ``
IMUL A,[377777,,1]ITEM 156 (Mitchell):
To make an AOBJN pointer when the origin is fixed and the length is a variable in A: ``
HRLOI A,-1(A)
EQVI A,ORIGINITEM 157 (Freiberg):
If instead, A is a pointer to the last word ``
HRLOI A,-ORIGIN(A)
EQVI A,ORIGINSlightly faster: change the HRLOIs to MOVSIs and the EQVI addresses to -ORIGIN-1. These two routines are clearly adjustable for BLKOs and other fenceposts.
ITEM 158 (Gosper, Salamin, Schroeppel):
A miniature (recursive) sine and cosine routine follows. ``
COS: FADR A,[1.57079632679] ;pi/2
SIN: MOVM B,A ;ARGUMENT IN A
CAMG B,[.00017] ; <= 3^(1/3) / 2^13
POPJ P, ;sin X = X, within 27. bits
FDVRI A,(-3.0)
PUSHJ P,SIN ;sin -X/3
FMPR B,B
FSC B,2
FADRI B,(-3.0)
FMPRB A,B ;sin X = 4(sin -X/3)^3 - 3(sin -X/3)
POPJ P, ;sin in A, sin or |sin| in B
;|sin| in B occurs when angle is smaller than end testChanging both -3.0's to +3.0's gives sinh:
sinh X = 3 sinh X/3 + 4 (sinh X/3)^3.
Changing the first -3.0 to a +9.0, then inserting PUSHJ P,.+1 after PUSHJ P,SIN gains about 20% in speed and uses half the pushdown space (< 5 levels in the first 4 quadrants). PUSHJ P,.+1 is a nice way to have something happen twice. Other useful angle multiplying formulas are
tanh X = (2 tanh X/2) / (1 + (tanh X/2)^2)
tan X = (2 tan X/2) / (1 - (tan X/2)^2),
if infinity is handled correctly. For cos and cosh, one can use
cos X = 1 - 2 (sin X/2)^2, cosh X = 1 + 2 (sinh X/2)^2.
In general, to compute functions like e^X, cos X, elliptic functions, etc. by iterated application of double and triple argument formulas, it is necessary to subtract out the constant in the Taylor series and transform the range reduction formula accordingly. Thus:
F(X) = cos(X)-1 F(2 X) = 2 F(F+2) F(epsilon) = -epsilon*^2/2
G(X) = e^X - 1 G(2 X) = G(G+2) G(epsilon) = epsilon*
This is to prevent the destruction of the information in the range-reduced argument by the addition of a quantity near 1 upon the success of the epsilon test. The addition of such a quantity in the actual recurrences is OK since the information is restored by the multiply. In fact, a cheap and dirty test for F(epsilon) sufficiently small is to see if the addition step has no effect. People lucky enough to have a square root instruction can get natural log by iterating
X <- X/(sqrt(1+X) + 1) until 1+X = 1.
Then multiply by 2^(number of iterations). Here, a LSH or FSC would work.
ITEM 159 (Gosper, Schroeppel):
(Numbers herein are decimal.)
The correct epsilon test in such functions as the foregoing SIN are generally the largest argument for which addition of the second term has no effect on the first. In SIN, the first term is x and the second is -x^3/6, so the answer is roughly the x which makes the ratio of those terms 1/2^27; so x = sqrt(3) / 2^13. But this is not exact, since the precise cutoff is where the neglected term is the power of 2 whose 1 bit coincides with the first neglected (28th) bit of the fraction. Thus, x^3/6 = 1/2^27 * 1/2^13, so x = 3^(1/3) / 2^13.
ITEM 160 (Gosper):
Here is a way to get log base 2. A and B are consecutive. Call by PUSHJ P,LOG2 with a floating point argument in A. ``
LOG2: LSHC A,-33
MOVSI C,-201(A)
TLC C,211000 ;Speciner's bum
MOVI A,200 ;exponent and sign sentinel
LOGL: LSH B,-9
REPEAT 7, FMPR B,B ;moby flunderflo
LSH B,2
LSHC A,7
SOJG A,LOGL ;fails on 4th try
LSH A,-1
FADR A,C
POPJ P, ;answer in ABasically you just square seven times and use the low seven bits of the exponent as the next seven bits of the log.
ITEM 161 (Gosper):
To swap the contents of two locations in memory: ``
EXCH A,LOC1
EXCH A,LOC2
EXCH A,LOC1Note: LOC1 must not equal LOC2! If this can happen use MOVE-EXCH-MOVEM, clobbering A.
ITEM 162 (Gosper):
To swap two bits in an accumulator: ``
TRCE A,BITS
TRCE A,BITS
TRCE A,BITSNote (Nelson): last TRCE never skips, and used to be a TRC, but TRCE is less forgettable. Also, use TLCE or TDCE if the bits are not in the right half.
ITEM 163 (Sussman):
To exchange two variables in LISP without using a third variable:
(SETQ X (PROG2 0 Y (SETQ Y X)))
ITEM 164 (Samson):
To take MAX in A of two byte pointers (where A and B are consecutive accumulators): ``
ROTC A,6
CAMG A,B
EXCH A,B
ROTC A,-6ITEM 165 (Freiberg):
A byte pointer can be converted to a character address < 2^18 by MULI A,<# bytes/word> followed by SUBI B,1-<# b/w>(A). To get full word character address, use SUB into a magic table.
ITEM 166 (Gosper, Liknaitzky):
To rotate three consecutive accumulators N < 37. places: ``
ROTC A,N
ROT B,-N
ROTC B,NThus M AC's can be ROTC'ed in 2M-3 instructions. (Stallman): For 73. > N > 35.: ``
ROTC A,N-36.
EXCH A,C
ROT B,36.-N
ROTC A,N-72.ITEM 167 (Gosper, Freiberg):
``
;B gets 7 bit character in A with even parity
IMUL A,[2010040201] ;5 adjacent copies
AND A,[21042104377] ;every 4th bit of left 4 copies + right copy
IDIVI A,17<-7 ;casting out 15.'s in hexadecimal shifted 7
;odd parity on 7 bits (Schroeppel)
IMUL A,[10040201] ;4 adjacent copies
IOR A,[7555555400] ;leaves every 3rd bit+offset+right copy
IDIVI A,9<-7 ;powers of 2^3 are +-1 mod 9
;changing 7555555400 to 27555555400 gives even parity
;if A is a 9 bit quantity, B gets number of 1's (Schroeppel)
IMUL A,[1001001001] ;4 copies
AND A,[42104210421] ;every 4th bit
IDIVI A,17 ;casting out 15.'s in hexadecimal
;if A is 6 bit quantity, B gets 6 bits reversed (Schroeppel)
IMUL A,[2020202] ;4 copies shifted
AND A,[104422010] ;where bits coincide with reverse repeated base 2^8
IDIVI A,377 ;casting out 2^8 - 1's
;reverse 7 bits (Schroeppel)
IMUL A,[10004002001] ;4 copies sep by 000's base 2 (may set arith. o'flow)
AND A,[210210210010] ;where bits coincide with reverse repeated base 2^8
IDIVI A,377 ;casting out 377's
;reverse 8 bits (Schroeppel)
MUL A,[100200401002] ;5 copies in A and B
AND B,[20420420020] ;where bits coincide with reverse repeated base 2^10
ANDI A,41 ;"
DIVI A,1777 ;casting out 2^10 - 1'sITEM 168 (PDP-1 hackers):
``
foo, lat /DATAI switches
adm a /ADDB
and (707070
adm b
iot 14 /output AC sign bit to a music flip-flop
jmp fooMakes startling chords, arpeggios, and slides, with just the sign of the AC. This translates to the PDP-6 (roughly) as: ``
FOO: DATAI 2
ADDB 1,2
AND 2,[707070707070] ;or 171717171717, 363636363636, 454545454545, ...
ADDB 2,3
LDB 0,[360600,,2]
JRST FOOListen to the square waves from the low bits of 0.
ITEM 169 (in order of one-ups-manship: Gosper, Mann, Lenard, [Root and Mann]):
To count the ones in a PDP-6/10 word: ``
LDB B,[014300,,A] ;or MOVE B,A then LSH B,-1
AND B,[333333,,333333]
SUB A,B
LSH B,-1
AND B,[333333,,333333]
SUBB A,B ;each octal digit is replaced by number of 1's in it
LSH B,-3
ADD A,B
AND A,[070707,,070707]
IDIVI A,77 ;casting out 63.'sThese ten instructions, with constants extended, would work on word lengths up to 62.; eleven suffice up to 254..
ITEM 170 (Jensen):
Useful strings of non-digits and zeros can arise when carefully chosen negative numbers are fed to unsuspecting decimal print routines. Different sets arise from different methods of character-to-digit conversion. Example (Gosper): ``
DPT: IDIVI F,12
HRLM G,(P) ;tuck remainder on pushdown list
SKIPE F
PUSHJ P,DPT
LDB G,[220600,,(P)] ;retrieve low 6 bits of remainder
TRCE G,"0 ;convert digit to character
SETOM CCT ;that was no digit!
TYO: .IOT TYOCHN,G ;or DATA0 or IDPB ...
AOS G,CCT
POPJ P,This is the standard recursive decimal print of the positive number in F, but with a LDB instead of a HLRZ. It falls into the typeout routine which returns in G the number of characters since the last carriage return. When called with a -36., DPT types carriage return, line feed, and resets CCT, the character position counter.
ITEM 171 (Gosper):
Since integer division can never produce a larger quotient than dividend, doubling the dividend and divisor beforehand will distinguish division by zero from division by 1 or anything else, in situations where division by zero does nothing.
ITEM 172 (Gosper):
The fundamental operation for building list structure, called CONS, is defined to: find a free cell in memory, store the argument in it, remove it from the set of free cells, return a pointer to it, and call the garbage collector when the set is empty. This can be done in two instructions: ``
CONS: EXCH A,[EXCH A,[...[PUSH P,GC]...]]
EXCH A,CONSOf course, the address-linked chain of EXCH's indicated by the nested brackets is concocted by the garbage collector. This method has the additional advantage of not constraining an accumulator for the free storage pointer. ``
UNCONS: HRLI A,(EXCH A,)
EXCH A,CONS
EXCH A,@CONSReturns cell addressed by A to free storage list; returns former cell contents in A.
ITEM 173 (Gosper):
The incantation to fix a floating number is usually ``
MULI A,400 ;exponent to A, fraction to A+1
TSC A,A ;1's complement magnitude of excess 200 exponent
ASH A+1,-200-27.-8(A) ;answer in A+1If number is known positive, you can omit the TSC.
On the PDP-10 ``
UFA A,[+-233000,,] ;not in PDP-6 repertoire
TLC A+1,233000 ;if those bits really bother youWhen you know the sign of A, and |A| < 2^26, you can ``
FAD A,[+-233400,,] ;or FADR for rounded fix!
TLC A,233400 ;if those bits are relevantwhere the sign of the constant must match A's. This works on both machines and doesn't involve A+1. On the 10, FADRI saves a cycle and a constant, and rounds.
ITEM 174 (Gosper, Nelson):
21963283741 . = 243507216435 is a fixed point of the float function on the PDP-6/10, i.e., it is the only positive number whose floating point representation equals its fixed.
ITEM 175 (Gosper):
To get the next higher number (in A) with the same number of 1 bits: (A, B, C, D do not have to be consecutive) ``
MOVE B,A
MOVN C,B
AND C,B
ADD A,C
MOVE D,A
XOR D,B
LSH D,-2
IDIVM D,C
IOR A,CPROGRAMMING ALGORITHMS, HEURISTICS
ITEM 176 (Gosper):
The "banana phenomenon" was encountered when processing a character string by taking the last 3 letters typed out, searching for a random occurrence of that sequence in the text, taking the letter following that occurrence, typing it out, and iterating. This ensures that every 4-letter string output occurs in the original. The program typed BANANANANANANANANA.... We note an ambiguity in the phrase, "the Nth occurrence of". In once sense, there are five 00's in 0000000000; in another, there are nine. The editing program TECO finds five. Thus it finds only the first ANA in BANANA, and is thus obligated to type N next. By Murphy's Law, there is but one NAN, thus forcing A, and thus a loop. An option to find overlapped instances would be useful, although it would require backing up N-1 characters before seeking the next N character string.
ITEM 177 (Gosper): DRAWING CURVES INCREMENTALLY
Certain plotters and displays are constrained to approximate curves by a sequence of king-moves between points on a lattice.
Many curves and contours are definable by F(X,Y) = 0 with F changing sign on opposite sides of the curve. The following algorithm will draw most such curves more accurately than polygonal approximations and more easily than techniques which search for a "next" X and Y just one move away.
We observe that a good choice of lattice points is just those for which F, when evaluated on one of them, has opposite sign and smaller magnitude than on one or more of its four immediate neighbors. This tends to choose the nearer endpoint of each graph paper line segment which the curve crosses, if near the curve F is monotone with distance from the curve.
First, divide the curve into arcs within which the curve's tangent lies within one 45 degree semiquadrant. We can show that for reasonable F, only two different increments (say north and northwest) are needed to visit the desired points.
Thus, we will be changing one coordinate (incrementing Y) every step, and we have only to check whether changing the other (decrementing X) will reduce the magnitude of F. (If F increases with Y, F(X,Y+1) > -F(X-1,Y+1) means decrement X.) F can often be manipulated so that the inequality simplifies and so that F is easily computed incrementally from X and Y.
As an example, the following computes the first semiquadrant of the circle
2 2 2
F = X + Y - R = 0.
C0: F <- 0, Y <- 0, X <- R
C1: F <- F+2Y+1, Y <- Y+1
C2: if F >= X, F <- F-2X+1, X <- X-1
C3: if Y < X-1, go to C1
C4: (Link to next arc) if Y = X-1, Y <- Y+1, X <- X-1This can be bummed by maintaining Z = 2Y+1 instead of Y. Symmetry may be used to compute all eight semiquadrants at once, or the loop may be closed at C2 and C3 with two PUSHJ's to provide the palindrome of decisions for the first quadrant. There is an expression for the number of steps per quadrant, but it has a three-way conditional dependent upon the midpoint geometry. Knowing this value, however, we can replace C3 and C4 with a simple loop count and an odd-even test for C4.
The loop must be top-tested (C3 before C1) if the "circle" R = 1, with four diagonal segments, is possible.
All this suggests that displays might be designed with an increment mode which accepts bit strings along with declarations of the form: "0 means north, 1 means northwest". 1100 (or 0011) will not occur with a curve of limited curvature; thus, it could be used as an escape code, but this would be an annoying restriction.
See the following illustration of circles drawn this way.
[In case of a tie, i.e., F has equal magnitudes with opposite signs on adjacent points, do not choose both points but rather have some arbitrary yet consistent preference for, say, the outer one. The problem can't arise for C2 in the example because the inequality F >= X is really F > -(F-2X+1) or F > X-.5.]
ITEM 178 (Schroeppel, Salamin):
Suppose Y satisfies a differential equation of the form
P(X) Y(Nth derivative) + ..... + Q(X) = R(X)where P, ..... Q, and R are polynomials in X
2 2 2
(for example, Bessel's equation, X Y'' + X Y' + (X - N ) Y = 0)and A is an algebraic number. Then Y(A) can be evaluated to N places in time proportional to N(ln N)^3.
Further, e^X and ln X or any elementary function can be evaluated to N places in N(ln N)^2 for X a real number. If F(X) can be evaluated in such time, so can the inverse of F(X) (by Newton's method), and the first derivative of F(X). Also, zeta(3) and gamma can be done in N(ln N)^3.
ITEM 179 (Gosper):
A program which searches a character string for a given substring can always be written by iterating the sequence fetch-compare-transfer (ILDB-CAIE-JRST on the PDP6/10) once for each character in the sought string. The destinations of the transfers (address fields of the JRST's) must, however, be computed as functions of the sought string. Let ``
0 1 2 3 4
S A S S Y
0 1 0 2 2stand for the program ``
T0: ILDB C,A ;C gets next char from pointer in A
T1: CAIE C,"S ;skip if it's an S
JRST T0 ;loop back on failure
ILDB C,A ;next
T2: CAIE C,"A ;skip if A
JRST T1 ;could be an S
ILDB C,A
T3: CAIE C,"S
JRST T0 ;S, A, non S, so start over
ILDB C,A
T4: CAIE C,"S
JRST T2 ;could be SAS.ASSY
ILDB C,A
CAIE C,"Y
JRST T2 ;could be SASS.ASSY
;found SASSYIn other words, a number > 0 in the top row is a location in the program where the corresponding letter of the middle row is compared with a character of the input string. If it differs, the number in the bottom row indicates the location where comparison is to resume. If it matches, the next character of the middle row is compared with the next character of the input string.
Let J be a number in the to row and K be the number below J, so that TK is the address field of the Jth JRST. For each J = 1, 2, ... we compute K(J) as follows: K(1) = 0. Let P be a counter, initially 0. For each succeeding J, increment P. If the Pth letter = the Jth, K(J) = K(P). Otherwise, K(J) = P, and P is reset to 0. (P(J) is the largest number such that the first P characters match the last P character in the first J characters of the sought string.) ``
J= 0 1 0 1 2 3 4 5
M I S S I S S I P P I I S S I S S I P P I
K(J)= 0 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 0 5 1 0
0 1 2 3 0 1 2 3
C O C A C O L A S A S S A F R A S
0 1 0 2 0 1 3 1 0 1 0 2 1 3 1 1 0To generalize this method to search for N strings at once, we produce a program of ILDB-CAIE-JRST's for each of the sought strings, omitting the initial ILDB from all but the first. We must compute the destination of the Jth JRST in the Ith program, TKM(I,J), which is the location of the Kth compare in the Mth program.
It might be reasonable to compile such an instruction sequence whenever a search is initiated, since alternative schemes usually require saving or backing up the character pointer.
ITEM 180 (Gosper):
A problem which may arise in machine processing of visual information is the identification of corners on a noisy boundary of a polygon. Assume you have a broken line. If it is a closed loop, find the vertex furthest from the centroid (or any place). Open the loop by making this place both endpoints and calling it a corner. We define the corner of a broken line segment to be the point the sum of whose distances from the endpoints is maximal. This will divide the segment in two, allowing us to proceed recursively, until our corner isn't much cornerier than the other along the line.
The perpendicular distance which the vector C lies from the line connecting the vectors A and B is just ``
(C - A) x (B - A)
----------------- ,
2 |A - B|but maximizing this can lose on very pointy V's. The distance sum hack can lose on very squashed Z's.
HARDWARE
ITEM 181 (Gosper):
A bug you might try to avoid when designing floating point hardware, relating to excess-200, 1's complement exponent, 2's complement fraction convention:
- An advantage is that negation and numerical comparison can be accomplished with the same instructions for both fixed and floating point numbers.
- A disadvantage is that the termination of the normalization process is ambiguous. Normally, when the sign bit unequals the highest bit of fraction, the number is normalized. A special case arises with negated powers of two. (That is, -(2^n), not (2)^-n.) Then the fraction is 400,,0 and the sign is - also.
This means it is necessary to check whether shifting left one more bit will bring in a one:
- if it brings in a zero, you will over-normalize
- if it brings in a one, you should do it
If you should but don't, rounding will un-normalize, and when you then re-normalize, the normalizing amount will be doubled, so you will be off by 2 smidgens (that is, the next to low order bit). Note that rounding can over-normalize as well as un-normalize, so you can't just stop normalization after rounding.
You might check this in your PDP-6/10. For example, combine 201400,,0+delta with minus 200777,,777777+2delta. For 0 <= delta <= 7777, the correct FMP result is minus 200777,,777776, and the correct FMPR result is minus 200777,,777777.
Over-normalized negative powers of 2 work in compares and most floating arithmetic. They lose with MOVN and as dividends. Unnormalized floating operands win completely on the PDP-10, except as divisors and dividends, the latter suffering truncation error.
ITEM 182 (Roe): VOLTAGE REGULATORS
Fairchild is now supplying positive voltage regulators costing about 2 dollars in lots of 1 (for example, the uA7805 for +5 volts).
ITEM 183 (Roe): CURRENT MIRRORS
The CA3083 (and CA3084) transistor arrays can be used to make neat current mirrors. (A current mirror supplies a current on one wire equal to that drawn from a second wire.)
ITEM 184 (Roe): ONE-SHOT
A dual MOS D-type flip-flop (such as the CD4013AE) can be used to make a one-shot as follows:
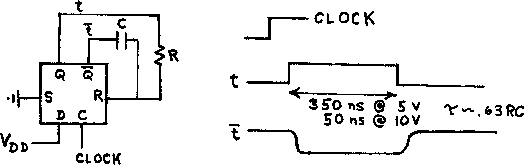
ITEM 185 (Roe): OSCILLATORS
Everyone has their own favorite oscillator circuits; here are some we like.
- I. crystal, overtone, transistor
- crystal, fundamental, transistor (drives at least 1 TTL load)
- crystal, fundamental, transistor (drives at least 1 TTL load)
- crystal, fundamental, CMOS, low frequency (drives 1 TTL load at 5.4 volts and no load, draws 330 microamperes; with a 165 KHz, 32 pf crystal, varies about 10 Hz per volt of Vcc)
- crystal, fundamental, CMOS, low frequency (drives 1 TTL load at 5.4 volts and no load, draws 330 microamperes; with a 165 KHz, 32 pf crystal, varies about 10 Hz per volt of Vcc)
- crystal, fundamental, IC (a favorite of Nelson's, but be careful and lucky or it may oscillate at a frequency determined by the crystal holder capacitance and not by the crystal; note similarity to non-crystal oscillator V)
- crystal, fundamental, IC (a favorite of Nelson's, but be careful and lucky or it may oscillate at a frequency determined by the crystal holder capacitance and not by the crystal; note similarity to non-crystal oscillator V)
- V. not crystal controlled; for comparison with IV
- The following blocking oscillator is quite uncritical of component values, with the exception that the turns ratio be such that -Vb (see graph) not exceed BVebo (about 5 volts for silicon transistors).
- The following blocking oscillator is quite uncritical of component values, with the exception that the turns ratio be such that -Vb (see graph) not exceed BVebo (about 5 volts for silicon transistors).
ITEM 186 (Roe): FM RADIO LINK
In work on education at our lab, we built a motorized "turtle" controlled by computer commands in the child-oriented language "Logo". The following is a transmitter designed as a radio link between the computer and turtle. Input (modulation) is either 0 or +1 volts; output is about 88MHz. Use a commercial FM tuner as receiver. Note: this transmitter is ILLEGAL no matter what; part 15 low power rule only allows if duty is less than about 1 second per 15 minutes. Don't worry about it unless you interfere with broadcast stations. 
ITEM 187 (Roe): PHONE LINE XMTR, RCVR
When the chess program written at our lab is playing in a chess tournament, a human attendant at the tournament moves the pieces, punches the clock, and communicates with the program via a portable terminal coupled to a telephone line. It is desirable that the program know when its chess clock is running, even though the attendant may not notice immediately that the opponent has made his move and punched the clock. Therefore we built a clock holder with a microswitch to sense the clock state. The following is a 10 mw transmitter whose input is the microswitch and whose output goes onto the phone line. It switches between two frequencies, about 320 and 470 Hz. Also shown is the receiver. Input should be at least 100 mv rms (threshold is 20 mv and overload is above 68 volts) with peak to peak signal to noise ration grater than 4:1. As we all know, connections to phone lines are illegal unless made through a data coupler supplied by TPC (The Phone Company).
ITEM 188 (Roe): DC MOTOR VELOCITY SERVO
One version of the "turtle" mentioned above (see RADIO LINK) uses a DC motor to drive each of its two powered wheels. since its path is to be as straight as possible, a triangular pulse is generated (to represent one "step" of the motor) and the motor's velocity servoed to this analog command. An additional digital command enables forward or reverse motion. Diagram I shows a simplified velocity servoing circuit. It has the disadvantage that only half the maximum voltage available (-V to +V) can be applied across the motor at any one time. Diagram II shows the actual circuit used in the turtle.
ITEM 189 (Roe): OPTICAL COUPLER
When two circuits are at potentials differing by a few hundred volts but wish to communicate with each other, one solutions is to use an optical coupler. these employ a light-emitting device placed close to a light-sensitive device. diodes make very fast-responding sensors, but the signal from a light-sensitive transistor is much stronger. shown is a compromise, using a transistor as a diode, with associated cleverness to get the delay (from input to output) down from 10 microseconds to 1.
ITEM 190 (Roe): PHOTOCATHODE CURRENT OSCILLATOR
In our fourth computer-interfaced image sensing device, TVD (really a vidissector, not a TV), the photocathode sits at several thousand volts negative. Nevertheless, one wishes to sense the current it draws, since overcurrent should shut down the photocathode voltage to avoid damage to the photocathode. The following circuit draws no more than 400 microamperes at 10 volts (at 20 KHz out; about 200 microamperes at 10 KHz) and couples the current information out as the frequency sent to T2, whose coils are wound on opposite sides of a ceramic ferrite.
ITEM 191 (Roe): DEFLECTION AMPLIFIER
TVD, mentioned above, uses a very carefully designed printed circuit amplifier to supply current to its magnetic deflection coils. Except for the notes with the diagram, we submit it without further explanation or cautions.
Notes:
Except where noted, resistors 10%, 1/4 watt.
Capacitances in microfarads/volts; electrolytics aluminum.
Diodes 1N4727, 1N4154, 1N4009 etc.; stored charge no more than 80 picocoulombs at 1 milliampere forward current.
1D103 = GE thermistor mounted at center of main heat sink.
220J = Analog Devices chopper amplifier.
- = temperature protection circuit (overtemperature cutout).
Q2, Q3, Q4, Q5, Q6, Q12,l Q13, Q14, Q15, Q16 mounted on one 1 Centigrade degree per watt heat sink (e.g., Wakefield 621K 1/2 inch in front of Rotron Muffin fan). Case temperature about 70 degrees C max. Ground heat sink and insulate transistors.
All transistors Motorola.
All zeners 1 watt.
VE48X = Varo; could be two 2 A 50 PIV fast recovery.
Output capacitance about 800 pf; damping R about 150 ohms for critical damping.
Slews from + (or -) 2 A to - (or +) 2 A in 4 microseconds; dE/dt is hot side of deflection coil is about a billion v/sec.
Layout is critical, as with most fast high-gain circuits.
- A By-passing and lead inductance: Short wide strips (or, better, a ground plane) should be used for ground bus, and ceramic capacitors with leads as short as practicable used for bypassing. Best bypass capacitor is Allen-Bradley CL series.
- B Ground loops: reference ground (triangles) and power ground must be interconnected only at the cold side of the sense resistor; take care to avoid stray current through the cold side of the signal input.
- C In general, the device should be constructed like a 144 MHz transmitter to avoid its becoming one.
The 100 pf stabilizing capacitor may want to be higher to decrease hunting and ringing, which could improve settling time more than the reduced gain-bandwidth would increase it.
Q1, Q12, Q13 MPS-U01
Q11, Q2, Q3 MPS-U51
Q4, Q5, Q6 2N5194
Q14, Q15, Q16 2N5191
Q7 MPS-U02
Q17 MPS-U52
Q8, Q19 2N3906
Q9, Q18 2N3904
- HAKMEM
- GEOMETRY, ALGEBRA, CALCULUS
- RECURRENCE RELATIONS
- BOOLEAN ALGEBRA
- RANDOM NUMBERS
- NUMBER THEORY, PRIMES, PROBABILITY
- ITEM 28 (Schroeppel):
- ITEM 29 (Schroeppel):
- ITEM 30 (Schroeppel):
- ITEM 31 (Schroeppel):
- ITEM 32 (Schroeppel):
- ITEM 33 (Schroeppel):
- ITEM 34 (Schroeppel):
- ITEM 35 (Schroeppel):
- ITEM 36 (Schroeppel):
- ITEM 37 (Gosper):
- ITEM 38 (Fredkin):
- ITEM 39 (Schutzenberger):
- ITEM 40 (Gosper):
- ITEM 41 (Salamin):
- ITEM 42 (Gosper):
- ITEM 43 (Schroeppel):
- ITEM 44 (Gosper):
- PROBLEM 45 (Gosper):
- ITEM 46 (Schroeppel):
- ITEM 47 (Beeler):
- ITEM 48 (Gosper, Schroeppel):
- ITEM 49:
- ITEM 50 (Schroeppel):
- ITEM 51 (Schroeppel):
- ITEM 52 (Salamin):
- ITEM 53 (Salamin):
- ITEM 54 (Salamin & Gosper):
- ITEM 55 (Schroeppel): GAUSSIAN INTEGERS
- ITEM 56 (Beeler):
- ITEM 57 (Beeler, Gosper):
- ITEM 58 (Fredkin):
- ITEM 59 (Schroeppel):
- ITEM 60 (Beeler):
- ITEM 61 (Root):
- ITEM 62 (Speciner):
- ITEM 63 (Schroeppel, etc.):
- AUTOMATA THEORY
- GAMES
- PROPOSED COMPUTER PROGRAMS, IN ORDER OF INCREASING RUNNING TIME (Schroeppel)
- CONTINUED FRACTIONS
- GROUP THEORY
- SET THEORY
- QUATERNIONS
- POLYOMINOS, ETC.
- TOPOLOGY
- SERIES
- FLOWS AND ITERATED FUNCTIONS
- PI
- PROGRAMMING HACKS
- ITEM 145 (Gosper):
- ITEM 146: MUNCHING SQUARES
- ITEM 147 (Schroeppel):
- ITEM 148 (Cohen, Beeler):
- ITEM 149 (Minsky): CIRCLE ALGORITHM
- ITEM 150 (Schroeppel):
- ITEM 151 (Gosper):
- ITEM 152 (Salamin):
- ITEM 153 (Minsky):
- ITEM 154 (Gosper):
- ITEM 155 (Liknaitzky):
- ITEM 156 (Mitchell):
- ITEM 157 (Freiberg):
- ITEM 158 (Gosper, Salamin, Schroeppel):
- ITEM 159 (Gosper, Schroeppel):
- ITEM 160 (Gosper):
- ITEM 161 (Gosper):
- ITEM 162 (Gosper):
- ITEM 163 (Sussman):
- ITEM 164 (Samson):
- ITEM 165 (Freiberg):
- ITEM 166 (Gosper, Liknaitzky):
- ITEM 167 (Gosper, Freiberg):
- ITEM 168 (PDP-1 hackers):
- ITEM 169 (in order of one-ups-manship: Gosper, Mann, Lenard, [Root and Mann]):
- ITEM 170 (Jensen):
- ITEM 171 (Gosper):
- ITEM 172 (Gosper):
- ITEM 173 (Gosper):
- ITEM 174 (Gosper, Nelson):
- ITEM 175 (Gosper):
- PROGRAMMING ALGORITHMS, HEURISTICS
- HARDWARE
- ITEM 181 (Gosper):
- ITEM 182 (Roe): VOLTAGE REGULATORS
- ITEM 183 (Roe): CURRENT MIRRORS
- ITEM 184 (Roe): ONE-SHOT
- ITEM 185 (Roe): OSCILLATORS
- ITEM 186 (Roe): FM RADIO LINK
- ITEM 187 (Roe): PHONE LINE XMTR, RCVR
- ITEM 188 (Roe): DC MOTOR VELOCITY SERVO
- ITEM 189 (Roe): OPTICAL COUPLER
- ITEM 190 (Roe): PHOTOCATHODE CURRENT OSCILLATOR
- ITEM 191 (Roe): DEFLECTION AMPLIFIER